Cyclic image generation using chaotic dynamics

Successive image generation using cyclic transformations is demonstrated by extending the CycleGAN model to transform images among three different categories. Repeated application of the trained generators produces sequences of images that transition among the different categories. The generated image sequences occupy a more limited region of the image space compared with the original training dataset. Quantitative evaluation using precision and recall metrics indicates that the generated images have high quality but reduced diversity relative to the training dataset. Such successive generation processes are characterized as chaotic dynamics in terms of dynamical system theory. Positive Lyapunov exponents estimated from the generated trajectories confirm the presence of chaotic dynamics, with the Lyapunov dimension of the attractor found to be comparable to the intrinsic dimension of the training data manifold. The results suggest that chaotic dynamics in the image space defined by the deep generative model contribute to the diversity of the generated images, constituting a novel approach for multi-class image generation. This model can be interpreted as an extension of classical associative memory to perform hetero-association among image categories.

Evaluating generation of chaotic time series by convolutional generative adversarial networks

To understand the ability and limitations of convolutional neural networks to generate time series that mimic complex temporal signals, we trained a generative adversarial network consisting of deep convolutional networks to generate chaotic time series and used nonlinear time series analysis to evaluate the generated time series. A numerical measure of determinism and the Lyapunov exponent, a measure of trajectory instability, showed that the generated time series well reproduce the chaotic properties of the original time series. However, error distribution analyses showed that large errors appeared at a low but non-negligible rate. Such errors would not be expected if the distribution were assumed to be exponential.

Functional differentiations in evolutionary reservoir computing networks

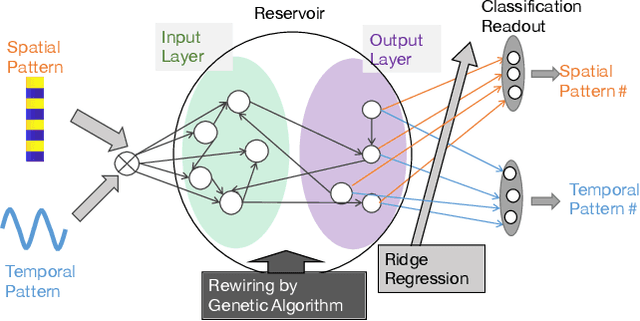
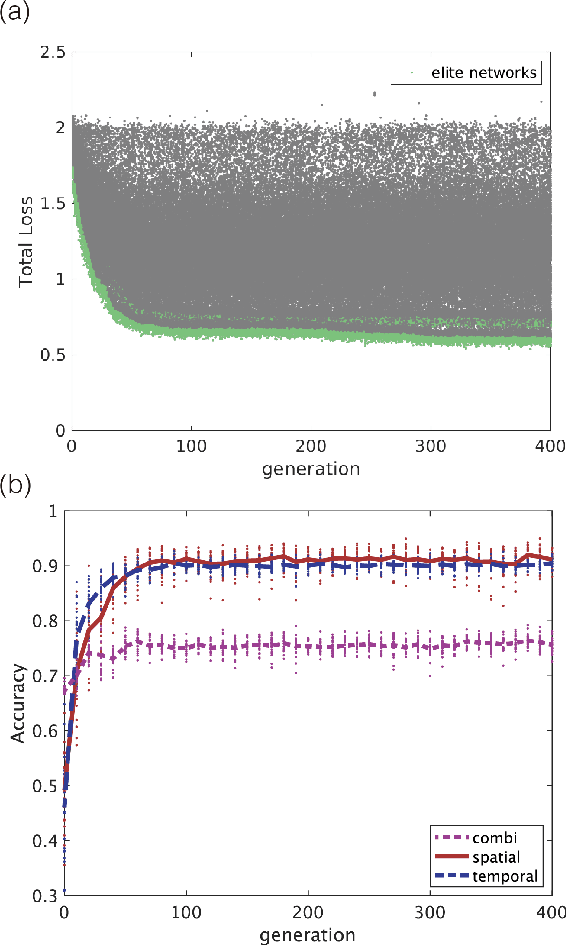
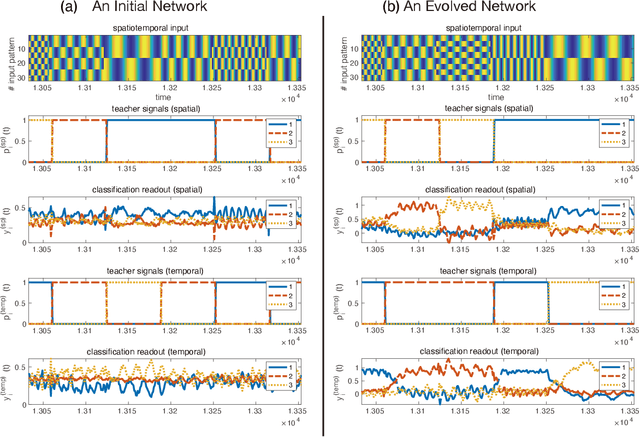
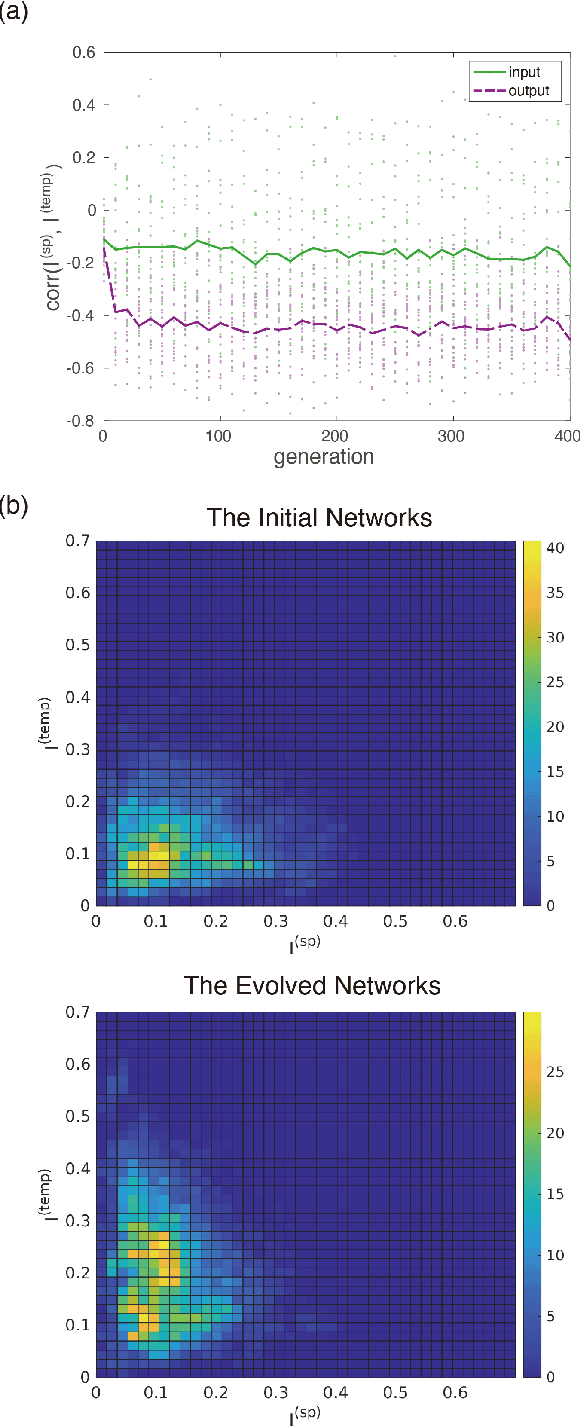
We propose an extended reservoir computer that shows the functional differentiation of neurons. The reservoir computer is developed to enable changing of the internal reservoir using evolutionary dynamics, and we call it an evolutionary reservoir computer. To develop neuronal units to show specificity, depending on the input information, the internal dynamics should be controlled to produce contracting dynamics after expanding dynamics. Expanding dynamics magnifies the difference of input information, while contracting dynamics contributes to forming clusters of input information, thereby producing multiple attractors. The simultaneous appearance of both dynamics indicates the existence of chaos. In contrast, sequential appearance of these dynamics during finite time intervals may induce functional differentiations. In this paper, we show how specific neuronal units are yielded in the evolutionary reservoir computer.