Less is More: some Computational Principles based on Parcimony, and Limitations of Natural Intelligence

Natural intelligence (NI) consistently achieves more with less. Infants learn language, develop abstract concepts, and acquire sensorimotor skills from sparse data, all within tight neural and energy limits. In contrast, today's AI relies on virtually unlimited computational power, energy, and data to reach high performance. This paper argues that constraints in NI are paradoxically catalysts for efficiency, adaptability, and creativity. We first show how limited neural bandwidth promotes concise codes that still capture complex patterns. Spiking neurons, hierarchical structures, and symbolic-like representations emerge naturally from bandwidth constraints, enabling robust generalization. Next, we discuss chaotic itinerancy, illustrating how the brain transits among transient attractors to flexibly retrieve memories and manage uncertainty. We then highlight reservoir computing, where random projections facilitate rapid generalization from small datasets. Drawing on developmental perspectives, we emphasize how intrinsic motivation, along with responsive social environments, drives infant language learning and discovery of meaning. Such active, embodied processes are largely absent in current AI. Finally, we suggest that adopting 'less is more' principles -- energy constraints, parsimonious architectures, and real-world interaction -- can foster the emergence of more efficient, interpretable, and biologically grounded artificial systems.

Trans-Bifurcation Prediction of Dynamics in terms of Extreme Learning Machines with Control Inputs

By extending the extreme learning machine by additional control inputs, we achieved almost complete reproduction of bifurcation structures of dynamical systems. The learning ability of the proposed neural network system is striking in that the entire structure of the bifurcations of a target one-parameter family of dynamical systems can be nearly reproduced by training on transient dynamics using only a few parameter values. Moreover, we propose a mechanism to explain this remarkable learning ability and discuss the relationship between the present results and similar results obtained by Kim et al.

Functional differentiations in evolutionary reservoir computing networks

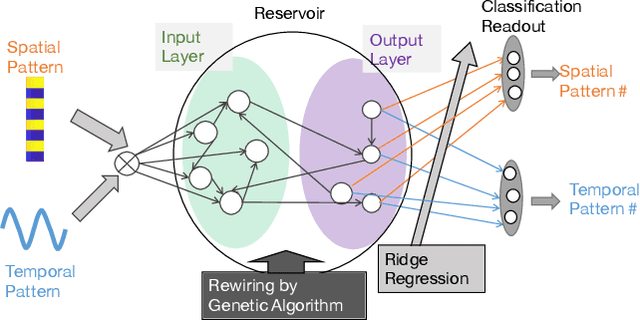
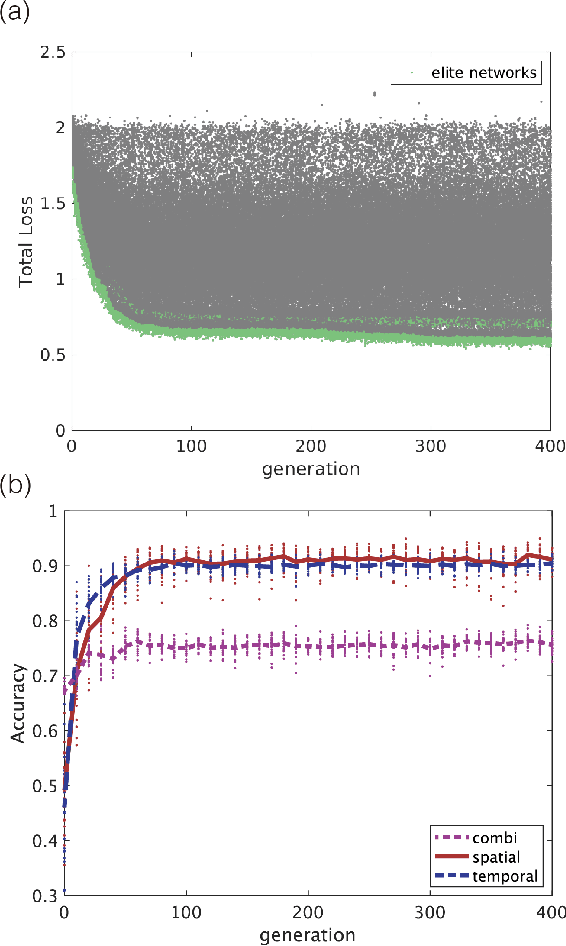
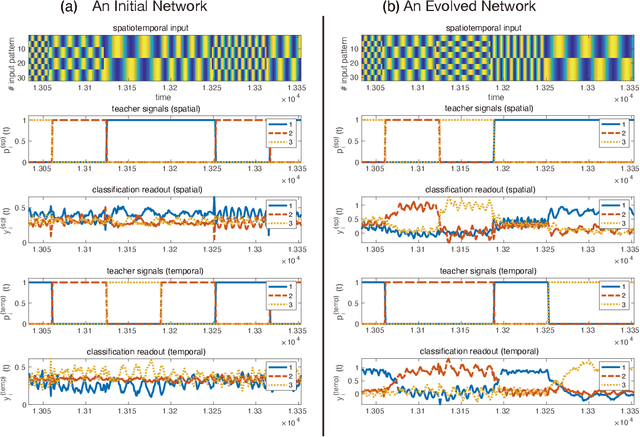
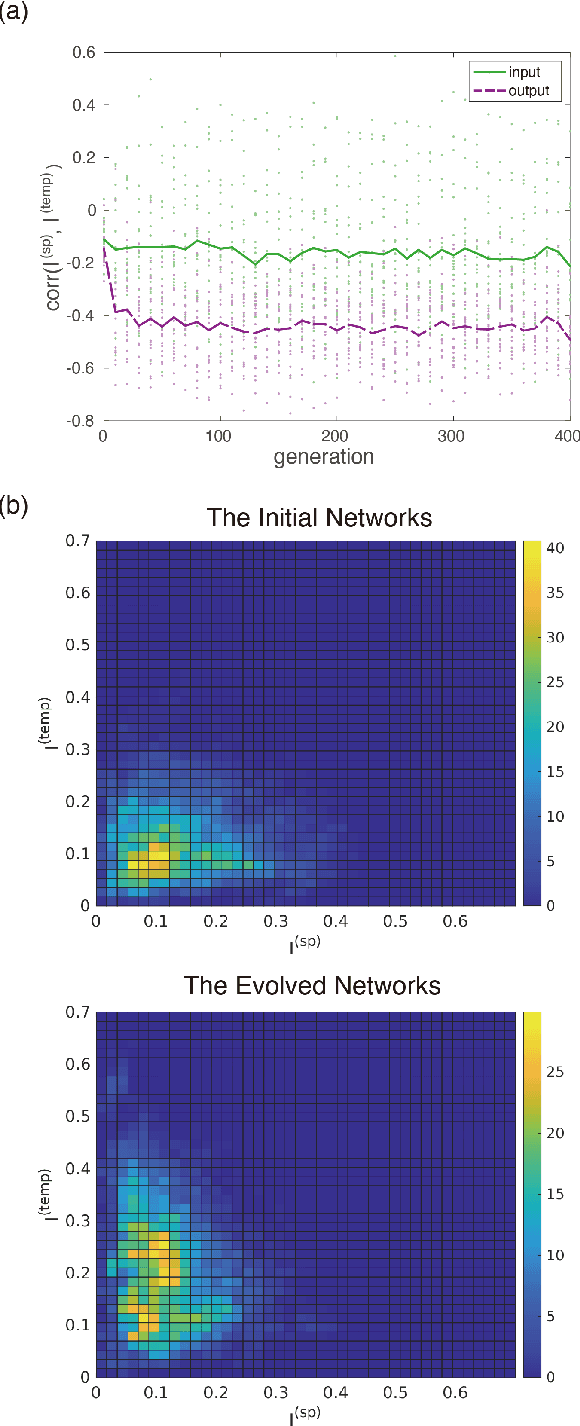
We propose an extended reservoir computer that shows the functional differentiation of neurons. The reservoir computer is developed to enable changing of the internal reservoir using evolutionary dynamics, and we call it an evolutionary reservoir computer. To develop neuronal units to show specificity, depending on the input information, the internal dynamics should be controlled to produce contracting dynamics after expanding dynamics. Expanding dynamics magnifies the difference of input information, while contracting dynamics contributes to forming clusters of input information, thereby producing multiple attractors. The simultaneous appearance of both dynamics indicates the existence of chaos. In contrast, sequential appearance of these dynamics during finite time intervals may induce functional differentiations. In this paper, we show how specific neuronal units are yielded in the evolutionary reservoir computer.