Analyzing the Runtime of the Gene-pool Optimal Mixing Evolutionary Algorithm (GOMEA) on the Concatenated Trap Function

The Gene-pool Optimal Mixing Evolutionary Algorithm (GOMEA) is a state of the art evolutionary algorithm that leverages linkage learning to efficiently exploit problem structure. By identifying and preserving important building blocks during variation, GOMEA has shown promising performance on various optimization problems. In this paper, we provide the first runtime analysis of GOMEA on the concatenated trap function, a challenging benchmark problem that consists of multiple deceptive subfunctions. We derived an upper bound on the expected runtime of GOMEA with a truthful linkage model, showing that it can solve the problem in $O(m^{3}2^k)$ with high probability, where $m$ is the number of subfunctions and $k$ is the subfunction length. This is a significant speedup compared to the (1+1) EA, which requires $O(ln{(m)}(mk)^{k})$ expected evaluations.

Modularity based linkage model for neuroevolution

Crossover between neural networks is considered disruptive due to the strong functional dependency between connection weights. We propose a modularity-based linkage model at the weight level to preserve functionally dependent communities (building blocks) in neural networks during mixing. A proximity matrix is built by estimating the dependency between weights, then a community detection algorithm maximizing modularity is run on the graph described by such matrix. The resulting communities/groups of parameters are considered to be mutually independent and used as crossover masks in an optimal mixing EA. A variant is tested with an operator that neutralizes the permutation problem of neural networks to a degree. Experiments were performed on 8 and 10-bit parity problems as the intrinsic hierarchical nature of the dependencies in these problems are challenging to learn. The results show that our algorithm finds better, more functionally dependent linkage which leads to more successful crossover and better performance.

Unimodal-uniform Constrained Wasserstein Training for Medical Diagnosis

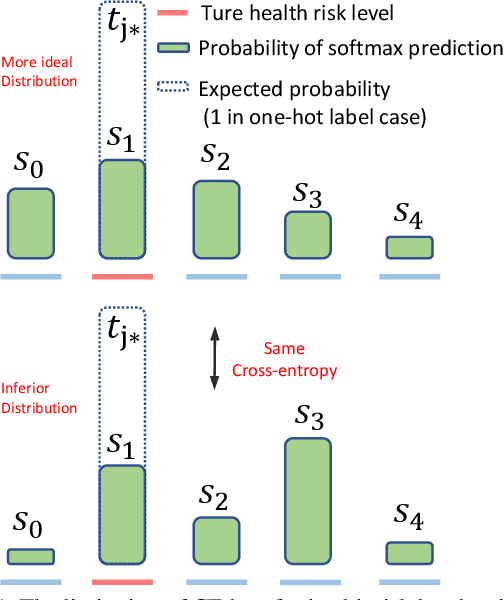
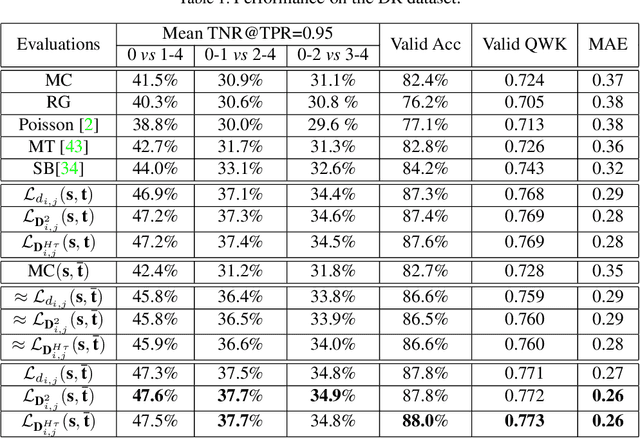
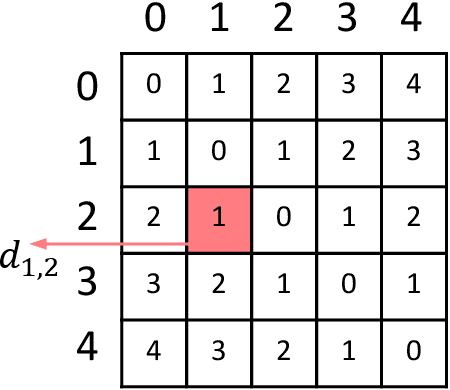
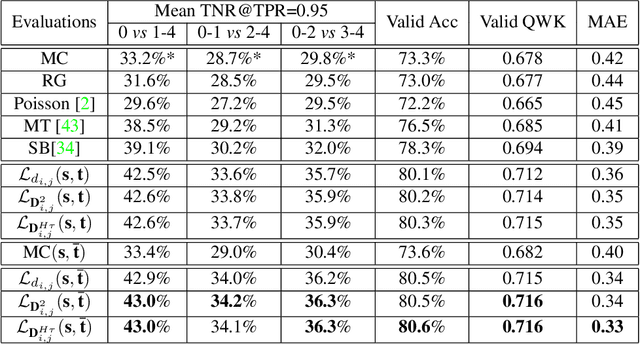
The labels in medical diagnosis task are usually discrete and successively distributed. For example, the Diabetic Retinopathy Diagnosis (DR) involves five health risk levels: no DR (0), mild DR (1), moderate DR (2), severe DR (3) and proliferative DR (4). This labeling system is common for medical disease. Previous methods usually construct a multi-binary-classification task or propose some re-parameter schemes in the output unit. In this paper, we target on this task from the perspective of loss function. More specifically, the Wasserstein distance is utilized as an alternative, explicitly incorporating the inter-class correlations by pre-defining its ground metric. Then, the ground metric which serves as a linear, convex or concave increasing function w.r.t. the Euclidean distance in a line is explored from an optimization perspective. Meanwhile, this paper also proposes of constructing the smoothed target labels that model the inlier and outlier noises by using a unimodal-uniform mixture distribution. Different from the one-hot setting, the smoothed label endues the computation of Wasserstein distance with more challenging features. With either one-hot or smoothed target label, this paper systematically concludes the practical closed-form solution. We evaluate our method on several medical diagnosis tasks (e.g., Diabetic Retinopathy and Ultrasound Breast dataset) and achieve state-of-the-art performance.