Leveraging Programmatically Generated Synthetic Data for Differentially Private Diffusion Training

Programmatically generated synthetic data has been used in differential private training for classification to enhance performance without privacy leakage. However, as the synthetic data is generated from a random process, the distribution of real data and the synthetic data are distinguishable and difficult to transfer. Therefore, the model trained with the synthetic data generates unrealistic random images, raising challenges to adapt the synthetic data for generative models. In this work, we propose DP-SynGen, which leverages programmatically generated synthetic data in diffusion models to address this challenge. By exploiting the three stages of diffusion models(coarse, context, and cleaning) we identify stages where synthetic data can be effectively utilized. We theoretically and empirically verified that cleaning and coarse stages can be trained without private data, replacing them with synthetic data to reduce the privacy budget. The experimental results show that DP-SynGen improves the quality of generative data by mitigating the negative impact of privacy-induced noise on the generation process.

BayesNAM: Leveraging Inconsistency for Reliable Explanations

Neural additive model (NAM) is a recently proposed explainable artificial intelligence (XAI) method that utilizes neural network-based architectures. Given the advantages of neural networks, NAMs provide intuitive explanations for their predictions with high model performance. In this paper, we analyze a critical yet overlooked phenomenon: NAMs often produce inconsistent explanations, even when using the same architecture and dataset. Traditionally, such inconsistencies have been viewed as issues to be resolved. However, we argue instead that these inconsistencies can provide valuable explanations within the given data model. Through a simple theoretical framework, we demonstrate that these inconsistencies are not mere artifacts but emerge naturally in datasets with multiple important features. To effectively leverage this information, we introduce a novel framework, Bayesian Neural Additive Model (BayesNAM), which integrates Bayesian neural networks and feature dropout, with theoretical proof demonstrating that feature dropout effectively captures model inconsistencies. Our experiments demonstrate that BayesNAM effectively reveals potential problems such as insufficient data or structural limitations of the model, providing more reliable explanations and potential remedies.

Leveraging Priors via Diffusion Bridge for Time Series Generation

Time series generation is widely used in real-world applications such as simulation, data augmentation, and hypothesis test techniques. Recently, diffusion models have emerged as the de facto approach for time series generation, emphasizing diverse synthesis scenarios based on historical or correlated time series data streams. Since time series have unique characteristics, such as fixed time order and data scaling, standard Gaussian prior might be ill-suited for general time series generation. In this paper, we exploit the usage of diverse prior distributions for synthesis. Then, we propose TimeBridge, a framework that enables flexible synthesis by leveraging diffusion bridges to learn the transport between chosen prior and data distributions. Our model covers a wide range of scenarios in time series diffusion models, which leverages (i) data- and time-dependent priors for unconditional synthesis, and (ii) data-scale preserving synthesis with a constraint as a prior for conditional generation. Experimentally, our model achieves state-of-the-art performance in both unconditional and conditional time series generation tasks.

Fair Sampling in Diffusion Models through Switching Mechanism

Diffusion models have shown their effectiveness in generation tasks by well-approximating the underlying probability distribution. However, diffusion models are known to suffer from an amplified inherent bias from the training data in terms of fairness. While the sampling process of diffusion models can be controlled by conditional guidance, previous works have attempted to find empirical guidance to achieve quantitative fairness. To address this limitation, we propose a fairness-aware sampling method called \textit{attribute switching} mechanism for diffusion models. Without additional training, the proposed sampling can obfuscate sensitive attributes in generated data without relying on classifiers. We mathematically prove and experimentally demonstrate the effectiveness of the proposed method on two key aspects: (i) the generation of fair data and (ii) the preservation of the utility of the generated data.

Differentially Private Sharpness-Aware Training

Training deep learning models with differential privacy (DP) results in a degradation of performance. The training dynamics of models with DP show a significant difference from standard training, whereas understanding the geometric properties of private learning remains largely unexplored. In this paper, we investigate sharpness, a key factor in achieving better generalization, in private learning. We show that flat minima can help reduce the negative effects of per-example gradient clipping and the addition of Gaussian noise. We then verify the effectiveness of Sharpness-Aware Minimization (SAM) for seeking flat minima in private learning. However, we also discover that SAM is detrimental to the privacy budget and computational time due to its two-step optimization. Thus, we propose a new sharpness-aware training method that mitigates the privacy-optimization trade-off. Our experimental results demonstrate that the proposed method improves the performance of deep learning models with DP from both scratch and fine-tuning. Code is available at https://github.com/jinseongP/DPSAT.

Improving the Utility of Differentially Private Clustering through Dynamical Processing

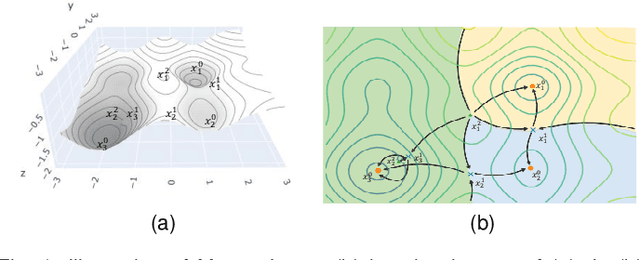
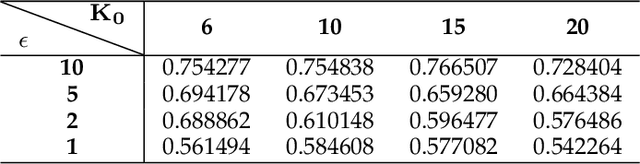
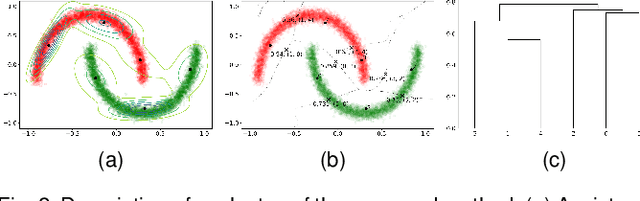
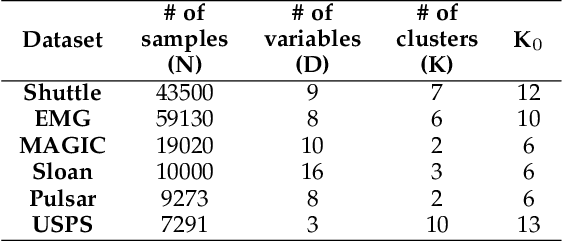
This study aims to alleviate the trade-off between utility and privacy in the task of differentially private clustering. Existing works focus on simple clustering methods, which show poor clustering performance for non-convex clusters. By utilizing Morse theory, we hierarchically connect the Gaussian sub-clusters to fit complex cluster distributions. Because differentially private sub-clusters are obtained through the existing methods, the proposed method causes little or no additional privacy loss. We provide a theoretical background that implies that the proposed method is inductive and can achieve any desired number of clusters. Experiments on various datasets show that our framework achieves better clustering performance at the same privacy level, compared to the existing methods.

Stability Analysis of Sharpness-Aware Minimization

Sharpness-aware minimization (SAM) is a recently proposed training method that seeks to find flat minima in deep learning, resulting in state-of-the-art performance across various domains. Instead of minimizing the loss of the current weights, SAM minimizes the worst-case loss in its neighborhood in the parameter space. In this paper, we demonstrate that SAM dynamics can have convergence instability that occurs near a saddle point. Utilizing the qualitative theory of dynamical systems, we explain how SAM becomes stuck in the saddle point and then theoretically prove that the saddle point can become an attractor under SAM dynamics. Additionally, we show that this convergence instability can also occur in stochastic dynamical systems by establishing the diffusion of SAM. We prove that SAM diffusion is worse than that of vanilla gradient descent in terms of saddle point escape. Further, we demonstrate that often overlooked training tricks, momentum and batch-size, are important to mitigate the convergence instability and achieve high generalization performance. Our theoretical and empirical results are thoroughly verified through experiments on several well-known optimization problems and benchmark tasks.