Oscillations enhance time-series prediction in reservoir computing with feedback

Reservoir computing, a machine learning framework used for modeling the brain, can predict temporal data with little observations and minimal computational resources. However, it is difficult to accurately reproduce the long-term target time series because the reservoir system becomes unstable. This predictive capability is required for a wide variety of time-series processing, including predictions of motor timing and chaotic dynamical systems. This study proposes oscillation-driven reservoir computing (ODRC) with feedback, where oscillatory signals are fed into a reservoir network to stabilize the network activity and induce complex reservoir dynamics. The ODRC can reproduce long-term target time series more accurately than conventional reservoir computing methods in a motor timing and chaotic time-series prediction tasks. Furthermore, it generates a time series similar to the target in the unexperienced period, that is, it can learn the abstract generative rules from limited observations. Given these significant improvements made by the simple and computationally inexpensive implementation, the ODRC would serve as a practical model of various time series data. Moreover, we will discuss biological implications of the ODRC, considering it as a model of neural oscillations and their cerebellar processors.

Compensated Integrated Gradients to Reliably Interpret EEG Classification

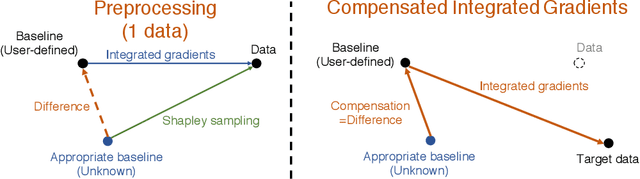
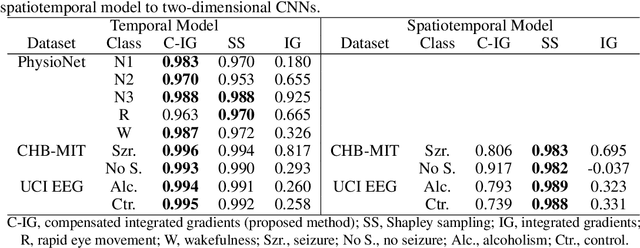
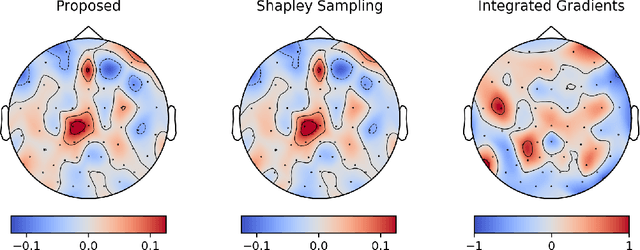
Integrated gradients are widely employed to evaluate the contribution of input features in classification models because it satisfies the axioms for attribution of prediction. This method, however, requires an appropriate baseline for reliable determination of the contributions. We propose a compensated integrated gradients method that does not require a baseline. In fact, the method compensates the attributions calculated by integrated gradients at an arbitrary baseline using Shapley sampling. We prove that the method retrieves reliable attributions if the processes of input features in a classifier are mutually independent, and they are identical like shared weights in convolutional neural networks. Using three electroencephalogram datasets, we experimentally demonstrate that the attributions of the proposed method are more reliable than those of the original integrated gradients, and its computational complexity is much lower than that of Shapley sampling.