Compensated Integrated Gradients to Reliably Interpret EEG Classification
Paper and Code
Nov 21, 2018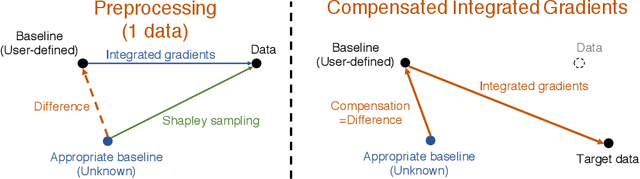
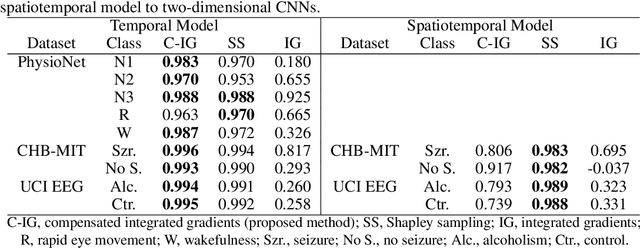
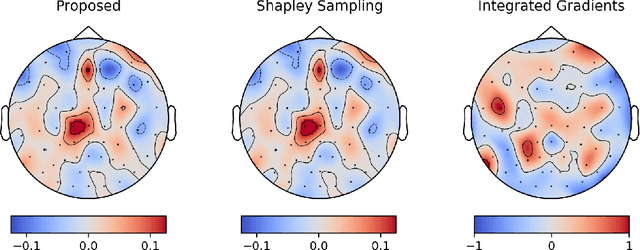
Integrated gradients are widely employed to evaluate the contribution of input features in classification models because it satisfies the axioms for attribution of prediction. This method, however, requires an appropriate baseline for reliable determination of the contributions. We propose a compensated integrated gradients method that does not require a baseline. In fact, the method compensates the attributions calculated by integrated gradients at an arbitrary baseline using Shapley sampling. We prove that the method retrieves reliable attributions if the processes of input features in a classifier are mutually independent, and they are identical like shared weights in convolutional neural networks. Using three electroencephalogram datasets, we experimentally demonstrate that the attributions of the proposed method are more reliable than those of the original integrated gradients, and its computational complexity is much lower than that of Shapley sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge