Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Yuhai Song
Learning Fast Approximations of Sparse Nonlinear Regression
Oct 26, 2020Figures and Tables: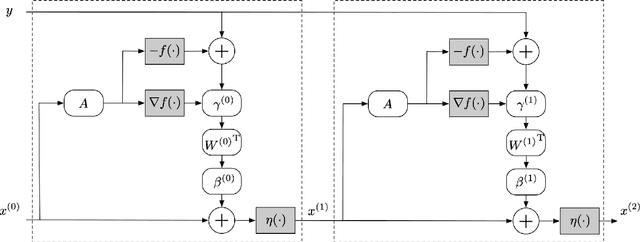

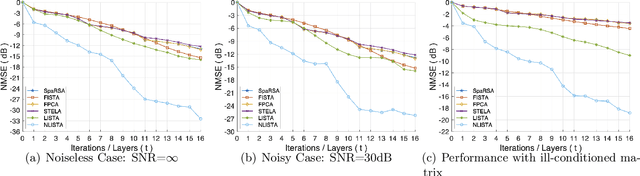



Abstract:The idea of unfolding iterative algorithms as deep neural networks has been widely applied in solving sparse coding problems, providing both solid theoretical analysis in convergence rate and superior empirical performance. However, for sparse nonlinear regression problems, a similar idea is rarely exploited due to the complexity of nonlinearity. In this work, we bridge this gap by introducing the Nonlinear Learned Iterative Shrinkage Thresholding Algorithm (NLISTA), which can attain a linear convergence under suitable conditions. Experiments on synthetic data corroborate our theoretical results and show our method outperforms state-of-the-art methods.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge