Yue Hui
Group Personalized Federated Learning
Oct 11, 2022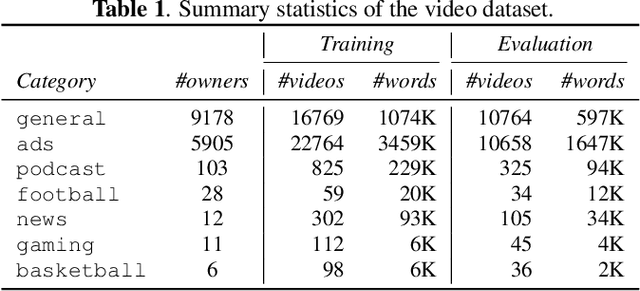
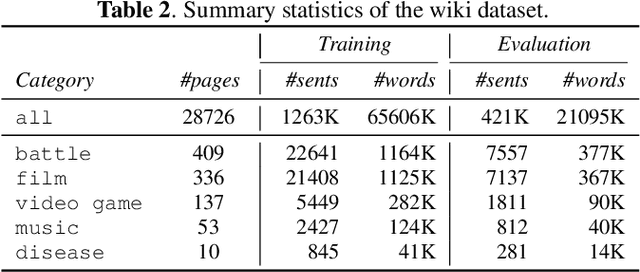
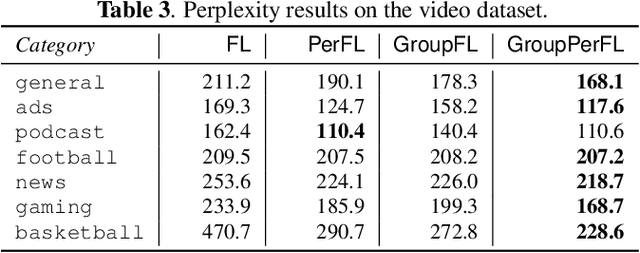
Abstract:Federated learning (FL) can help promote data privacy by training a shared model in a de-centralized manner on the physical devices of clients. In the presence of highly heterogeneous distributions of local data, personalized FL strategy seeks to mitigate the potential client drift. In this paper, we present the group personalization approach for applications of FL in which there exist inherent partitions among clients that are significantly distinct. In our method, the global FL model is fine-tuned through another FL training process over each homogeneous group of clients, after which each group-specific FL model is further adapted and personalized for any client. The proposed method can be well interpreted from a Bayesian hierarchical modeling perspective. With experiments on two real-world datasets, we demonstrate this approach can achieve superior personalization performance than other FL counterparts.
On the geometry of generalization and memorization in deep neural networks
May 30, 2021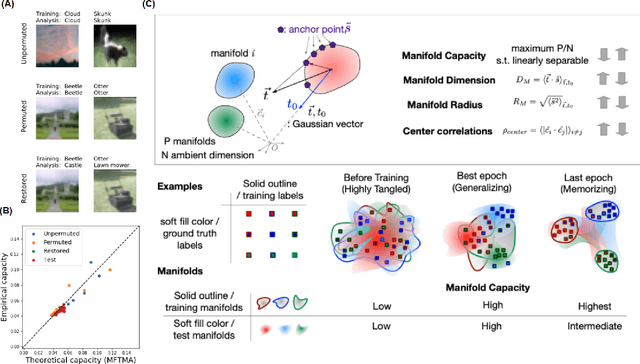
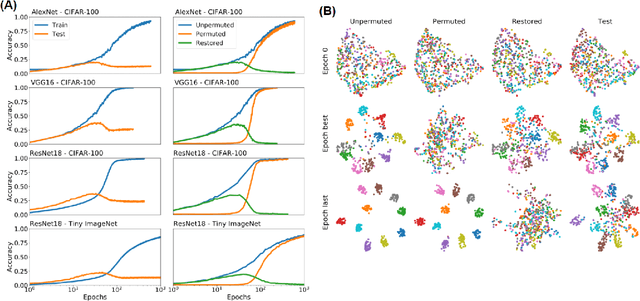
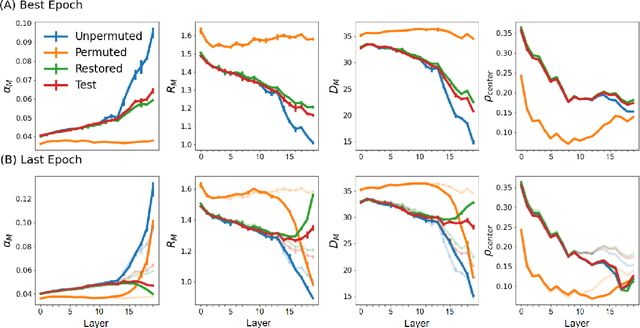
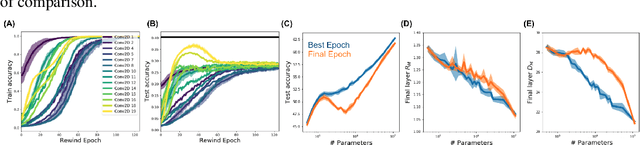
Abstract:Understanding how large neural networks avoid memorizing training data is key to explaining their high generalization performance. To examine the structure of when and where memorization occurs in a deep network, we use a recently developed replica-based mean field theoretic geometric analysis method. We find that all layers preferentially learn from examples which share features, and link this behavior to generalization performance. Memorization predominately occurs in the deeper layers, due to decreasing object manifolds' radius and dimension, whereas early layers are minimally affected. This predicts that generalization can be restored by reverting the final few layer weights to earlier epochs before significant memorization occurred, which is confirmed by the experiments. Additionally, by studying generalization under different model sizes, we reveal the connection between the double descent phenomenon and the underlying model geometry. Finally, analytical analysis shows that networks avoid memorization early in training because close to initialization, the gradient contribution from permuted examples are small. These findings provide quantitative evidence for the structure of memorization across layers of a deep neural network, the drivers for such structure, and its connection to manifold geometric properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge