Universal Online Learning with Gradual Variations: A Multi-layer Online Ensemble Approach

In this paper, we propose an online convex optimization method with two different levels of adaptivity. On a higher level, our method is agnostic to the specific type and curvature of the loss functions, while at a lower level, it can exploit the niceness of the environments and attain problem-dependent guarantees. To be specific, we obtain $\mathcal{O}(\ln V_T)$, $\mathcal{O}(d \ln V_T)$ and $\hat{\mathcal{O}}(\sqrt{V_T})$ regret bounds for strongly convex, exp-concave and convex loss functions, respectively, where $d$ is the dimension, $V_T$ denotes problem-dependent gradient variations and $\hat{\mathcal{O}}(\cdot)$-notation omits logarithmic factors on $V_T$. Our result finds broad implications and applications. It not only safeguards the worst-case guarantees, but also implies the small-loss bounds in analysis directly. Besides, it draws deep connections with adversarial/stochastic convex optimization and game theory, further validating its practical potential. Our method is based on a multi-layer online ensemble incorporating novel ingredients, including carefully-designed optimism for unifying diverse function types and cascaded corrections for algorithmic stability. Remarkably, despite its multi-layer structure, our algorithm necessitates only one gradient query per round, making it favorable when the gradient evaluation is time-consuming. This is facilitated by a novel regret decomposition equipped with customized surrogate losses.

Storage Fit Learning with Feature Evolvable Streams

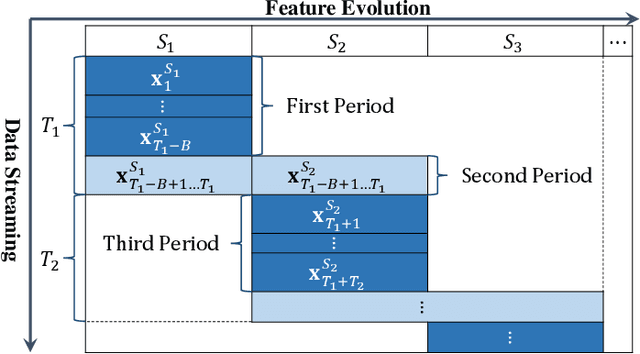
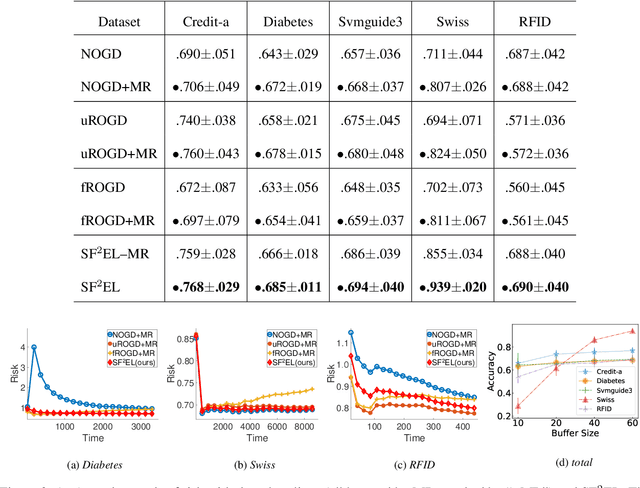
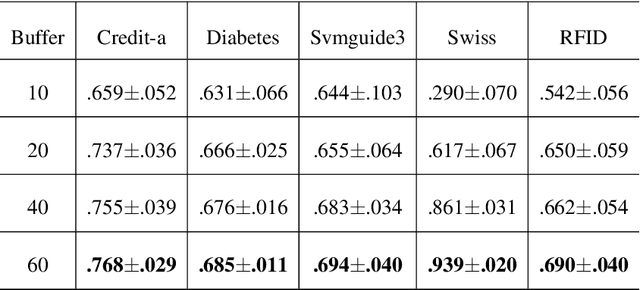
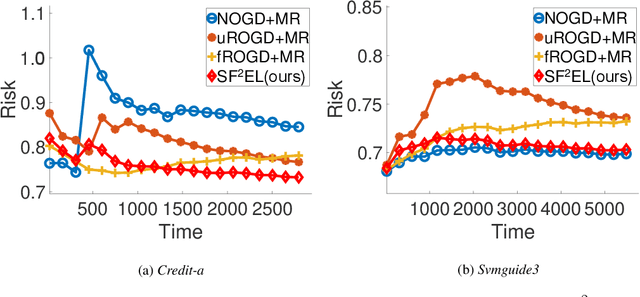
Feature evolvable learning has been widely studied in recent years where old features will vanish and new features will emerge when learning with streams. Conventional methods usually assume that a label will be revealed after prediction at each time step. However, in practice, this assumption may not hold whereas no label will be given at most time steps. To tackle this problem, we leverage the technique of manifold regularization to utilize the previous similar data to assist the refinement of the online model. Nevertheless, this approach needs to store all previous data which is impossible in learning with streams that arrive sequentially in large volume. Thus we need a buffer to store part of them. Considering that different devices may have different storage budgets, the learning approaches should be flexible subject to the storage budget limit. In this paper, we propose a new setting: Storage-Fit Feature-Evolvable streaming Learning (SF2EL) which incorporates the issue of rarely-provided labels into feature evolution. Our framework is able to fit its behavior to different storage budgets when learning with feature evolvable streams with unlabeled data. Besides, both theoretical and empirical results validate that our approach can preserve the merit of the original feature evolvable learning i.e., can always track the best baseline and thus perform well at any time step.