IPAD: Stable Interpretable Forecasting with Knockoffs Inference

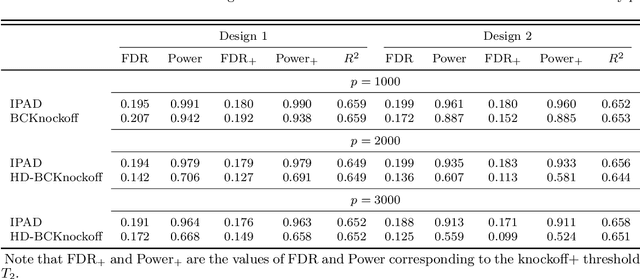
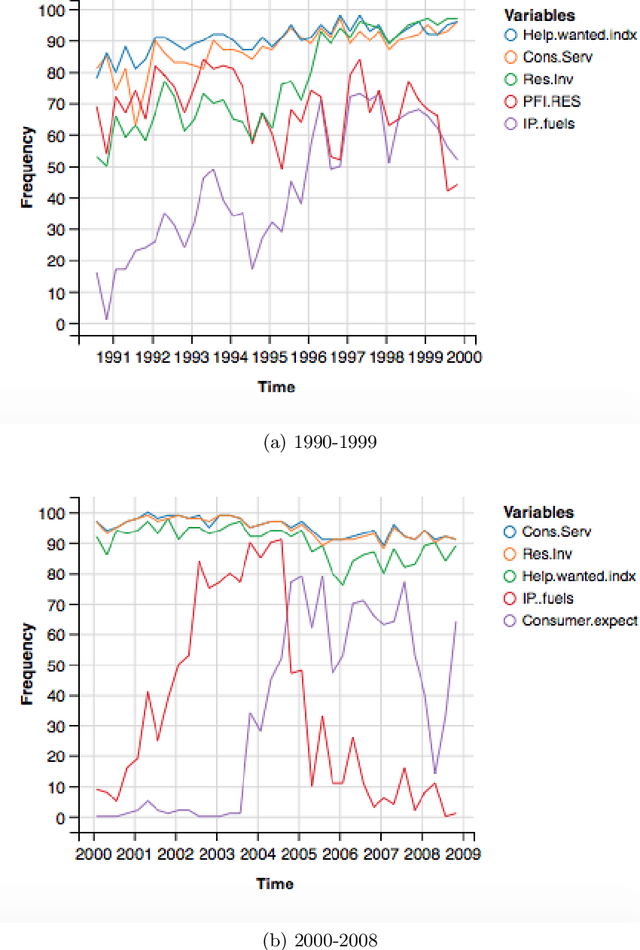
Interpretability and stability are two important features that are desired in many contemporary big data applications arising in economics and finance. While the former is enjoyed to some extent by many existing forecasting approaches, the latter in the sense of controlling the fraction of wrongly discovered features which can enhance greatly the interpretability is still largely underdeveloped in the econometric settings. To this end, in this paper we exploit the general framework of model-X knockoffs introduced recently in Cand\`{e}s, Fan, Janson and Lv (2018), which is nonconventional for reproducible large-scale inference in that the framework is completely free of the use of p-values for significance testing, and suggest a new method of intertwined probabilistic factors decoupling (IPAD) for stable interpretable forecasting with knockoffs inference in high-dimensional models. The recipe of the method is constructing the knockoff variables by assuming a latent factor model that is exploited widely in economics and finance for the association structure of covariates. Our method and work are distinct from the existing literature in that we estimate the covariate distribution from data instead of assuming that it is known when constructing the knockoff variables, our procedure does not require any sample splitting, we provide theoretical justifications on the asymptotic false discovery rate control, and the theory for the power analysis is also established. Several simulation examples and the real data analysis further demonstrate that the newly suggested method has appealing finite-sample performance with desired interpretability and stability compared to some popularly used forecasting methods.

SOFAR: large-scale association network learning

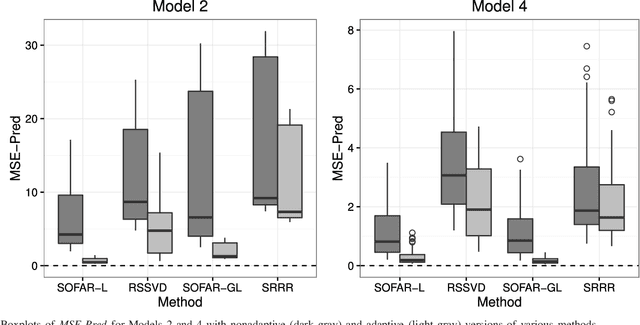
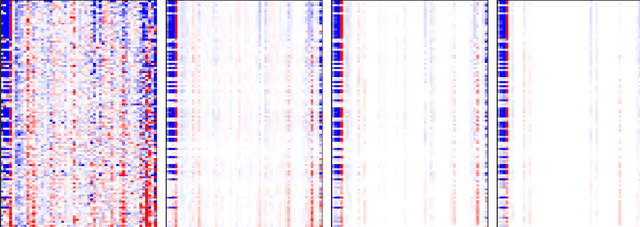
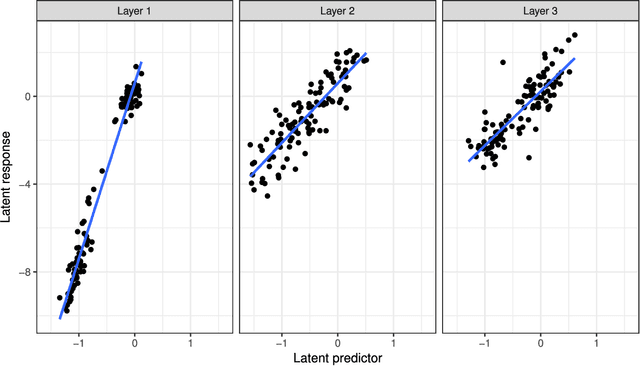
Many modern big data applications feature large scale in both numbers of responses and predictors. Better statistical efficiency and scientific insights can be enabled by understanding the large-scale response-predictor association network structures via layers of sparse latent factors ranked by importance. Yet sparsity and orthogonality have been two largely incompatible goals. To accommodate both features, in this paper we suggest the method of sparse orthogonal factor regression (SOFAR) via the sparse singular value decomposition with orthogonality constrained optimization to learn the underlying association networks, with broad applications to both unsupervised and supervised learning tasks such as biclustering with sparse singular value decomposition, sparse principal component analysis, sparse factor analysis, and spare vector autoregression analysis. Exploiting the framework of convexity-assisted nonconvex optimization, we derive nonasymptotic error bounds for the suggested procedure characterizing the theoretical advantages. The statistical guarantees are powered by an efficient SOFAR algorithm with convergence property. Both computational and theoretical advantages of our procedure are demonstrated with several simulation and real data examples.