MEGG: Replay via Maximally Extreme GGscore in Incremental Learning for Neural Recommendation Models

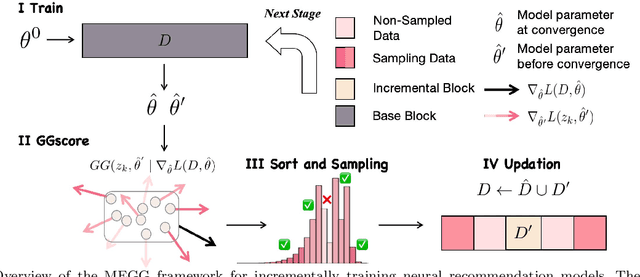
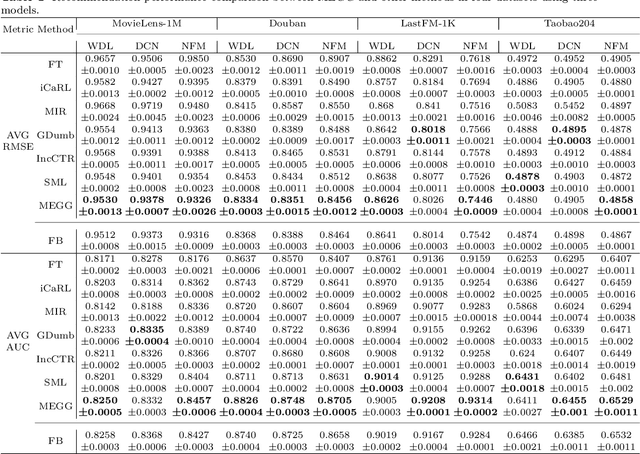
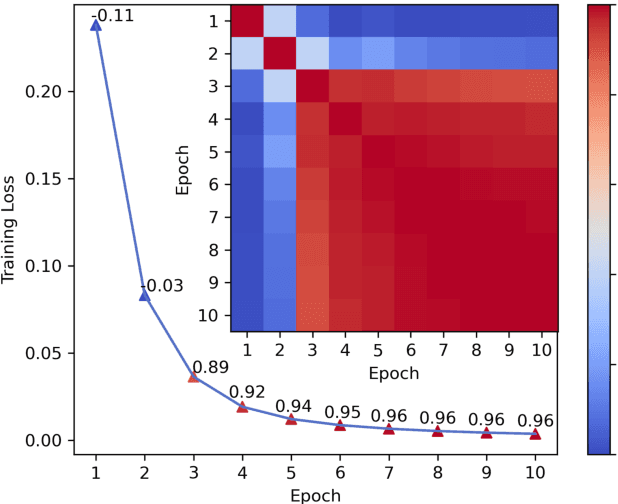
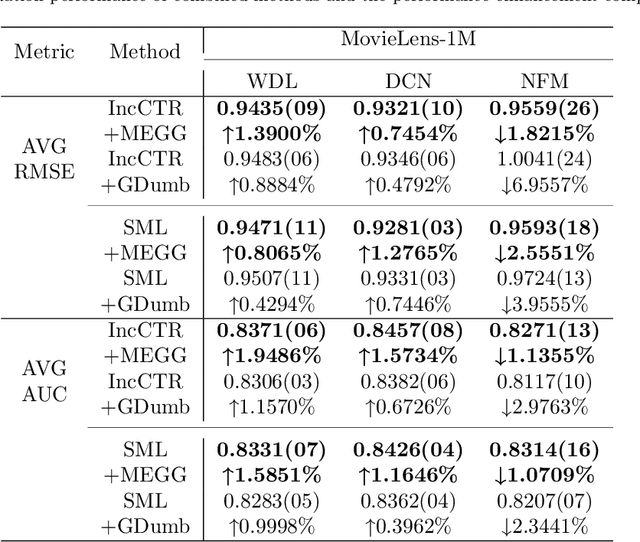
Neural Collaborative Filtering models are widely used in recommender systems but are typically trained under static settings, assuming fixed data distributions. This limits their applicability in dynamic environments where user preferences evolve. Incremental learning offers a promising solution, yet conventional methods from computer vision or NLP face challenges in recommendation tasks due to data sparsity and distinct task paradigms. Existing approaches for neural recommenders remain limited and often lack generalizability. To address this, we propose MEGG, Replay Samples with Maximally Extreme GGscore, an experience replay based incremental learning framework. MEGG introduces GGscore, a novel metric that quantifies sample influence, enabling the selective replay of highly influential samples to mitigate catastrophic forgetting. Being model-agnostic, MEGG integrates seamlessly across architectures and frameworks. Experiments on three neural models and four benchmark datasets show superior performance over state-of-the-art baselines, with strong scalability, efficiency, and robustness. Implementation will be released publicly upon acceptance.

Conditional Local Feature Encoding for Graph Neural Networks

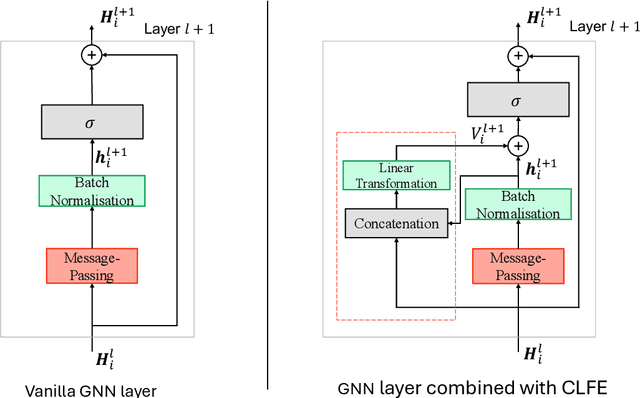
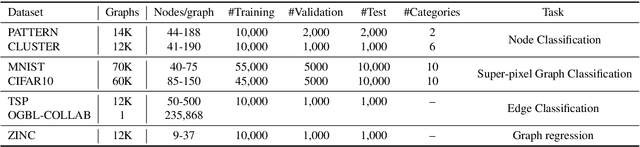
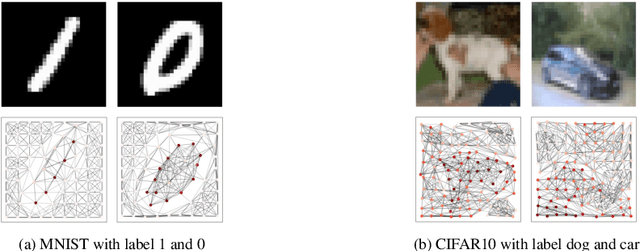
Graph neural networks (GNNs) have shown great success in learning from graph-based data. The key mechanism of current GNNs is message passing, where a node's feature is updated based on the information passing from its local neighbourhood. A limitation of this mechanism is that node features become increasingly dominated by the information aggregated from the neighbourhood as we use more rounds of message passing. Consequently, as the GNN layers become deeper, adjacent node features tends to be similar, making it more difficult for GNNs to distinguish adjacent nodes, thereby, limiting the performance of GNNs. In this paper, we propose conditional local feature encoding (CLFE) to help prevent the problem of node features being dominated by the information from local neighbourhood. The idea of our method is to extract the node hidden state embedding from message passing process and concatenate it with the nodes feature from previous stage, then we utilise linear transformation to form a CLFE based on the concatenated vector. The CLFE will form the layer output to better preserve node-specific information, thus help to improve the performance of GNN models. To verify the feasibility of our method, we conducted extensive experiments on seven benchmark datasets for four graph domain tasks: super-pixel graph classification, node classification, link prediction, and graph regression. The experimental results consistently demonstrate that our method improves model performance across a variety of baseline GNN models for all four tasks.