Epistasis-based Basis Estimation Method for Simplifying the Problem Space of an Evolutionary Search in Binary Representation

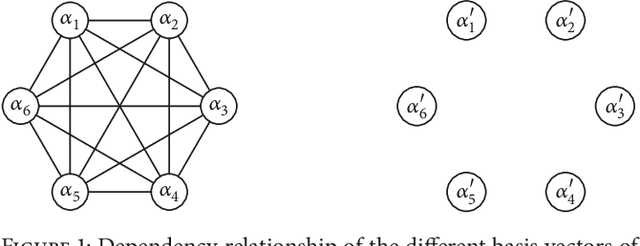
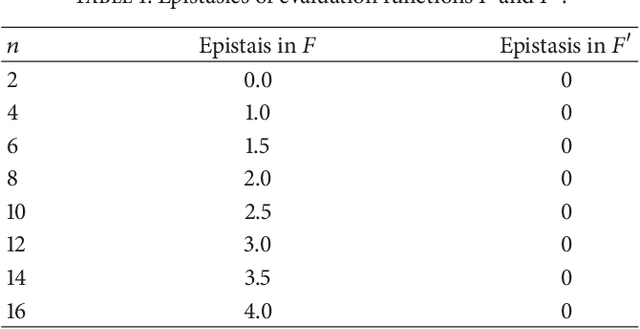
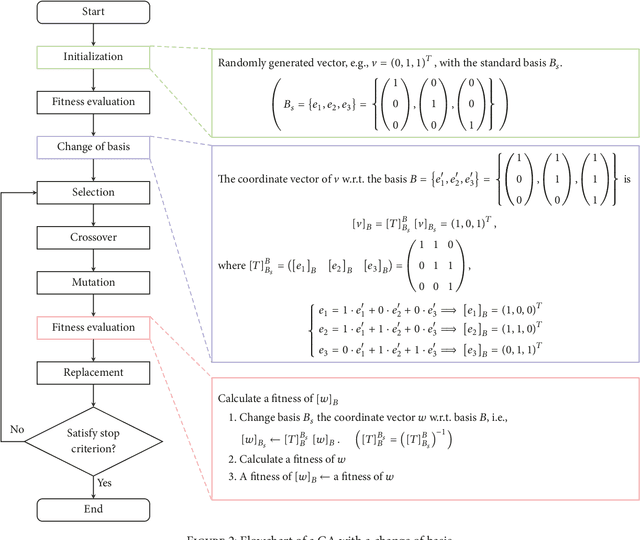
An evolutionary search space can be smoothly transformed via a suitable change of basis; however, it can be difficult to determine an appropriate basis. In this paper, a method is proposed to select an optimum basis can be used to simplify an evolutionary search space in a binary encoding scheme. The basis search method is based on a genetic algorithm and the fitness evaluation is based on the epistasis, which is an indicator of the complexity of a genetic algorithm. Two tests were conducted to validate the proposed method when applied to two different evolutionary search problems. The first searched for an appropriate basis to apply, while the second searched for a solution to the test problem. The results obtained after the identified basis had been applied were compared to those with the original basis, and it was found that the proposed method provided superior results.

Recent Progress on Graph Partitioning Problems Using Evolutionary Computation

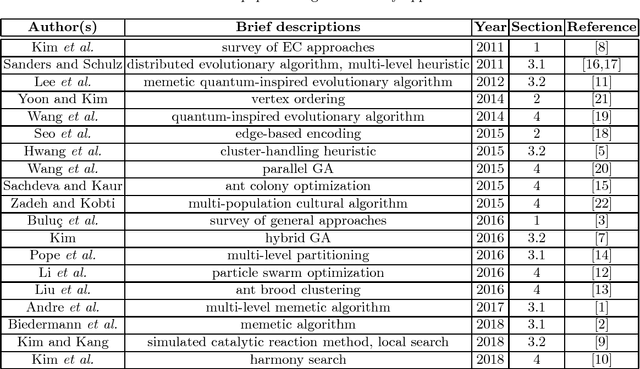
The graph partitioning problem (GPP) is a representative combinatorial optimization problem which is NP-hard. Currently, various approaches to solve GPP have been introduced. Among these, the GPP solution using evolutionary computation (EC) is an effective approach. There has not been any survey on the research applying EC to GPP since 2011. In this survey, we introduce various attempts to apply EC to GPP made in the recent seven years.

Charge Scheduling of an Energy Storage System under Time-of-use Pricing and a Demand Charge

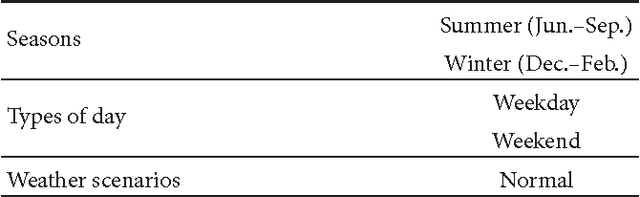
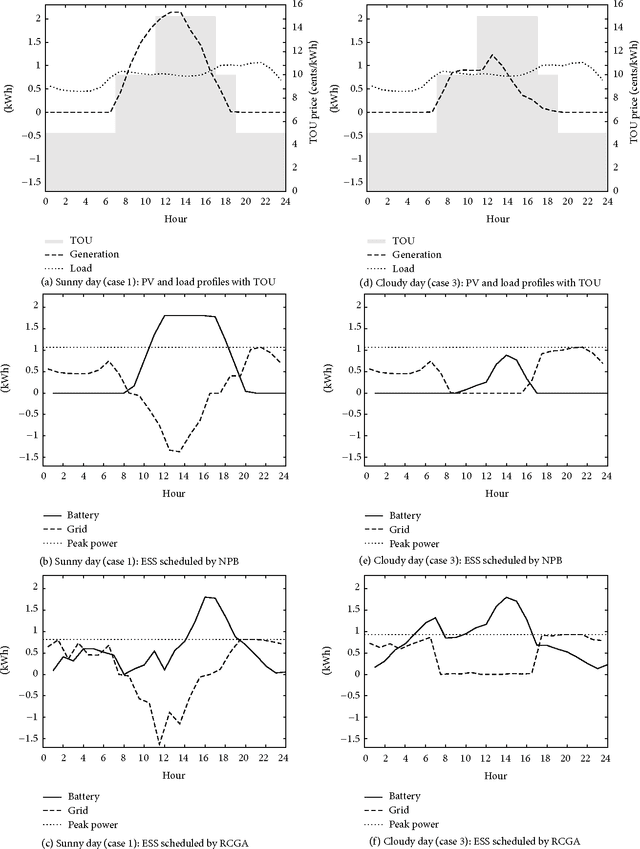
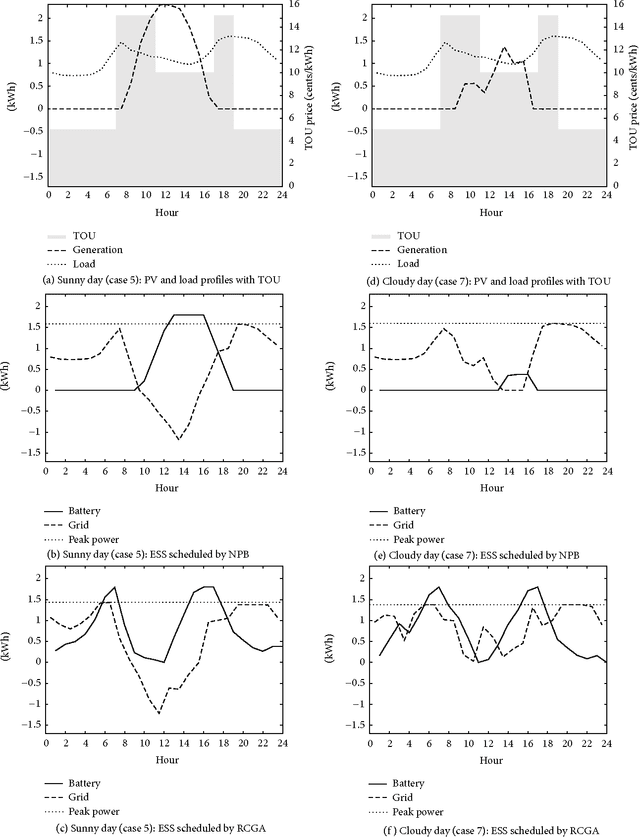
A real-coded genetic algorithm is used to schedule the charging of an energy storage system (ESS), operated in tandem with renewable power by an electricity consumer who is subject to time-of-use pricing and a demand charge. Simulations based on load and generation profiles of typical residential customers show that an ESS scheduled by our algorithm can reduce electricity costs by approximately 17%, compared to a system without an ESS, and by 8% compared to a scheduling algorithm based on net power.

Mathematical Interpretation between Genotype and Phenotype Spaces and Induced Geometric Crossovers

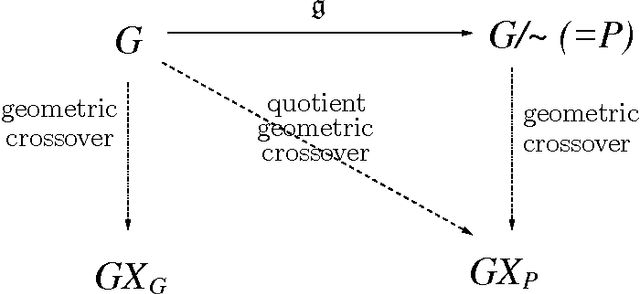
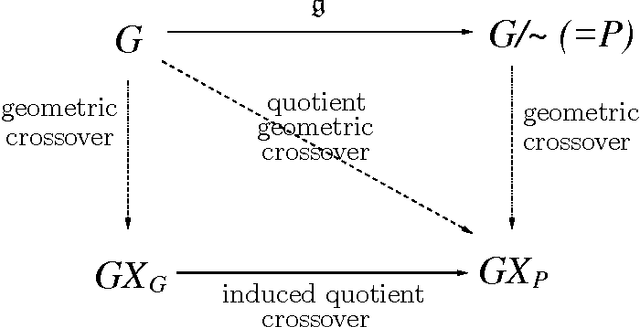
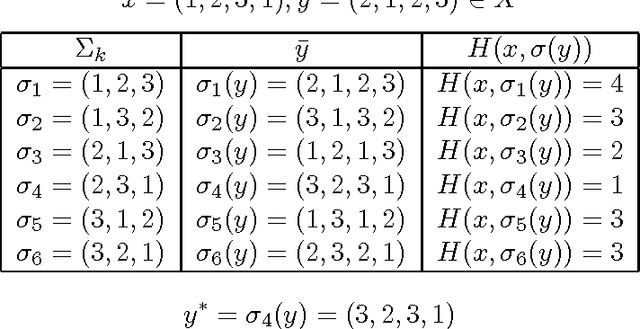
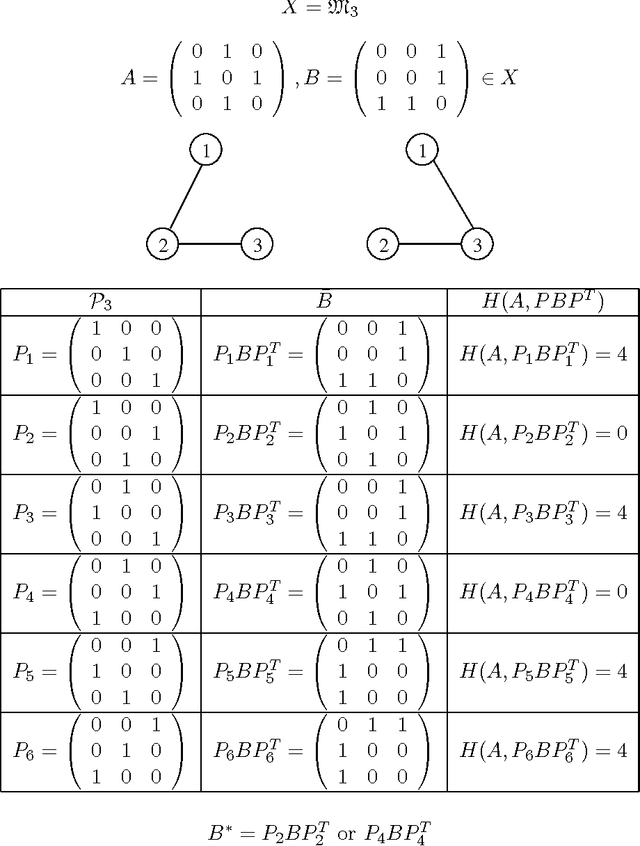
In this paper, we present that genotype-phenotype mapping can be theoretically interpreted using the concept of quotient space in mathematics. Quotient space can be considered as mathematically-defined phenotype space in the evolutionary computation theory. The quotient geometric crossover has the effect of reducing the search space actually searched by geometric crossover, and it introduces problem knowledge in the search by using a distance better tailored to the specific solution interpretation. Quotient geometric crossovers are directly applied to the genotype space but they have the effect of the crossovers performed on phenotype space. We give many example applications of the quotient geometric crossover.

A Mathematical Unification of Geometric Crossovers Defined on Phenotype Space

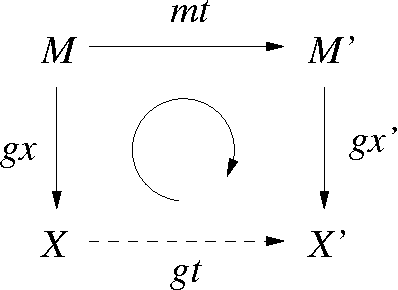
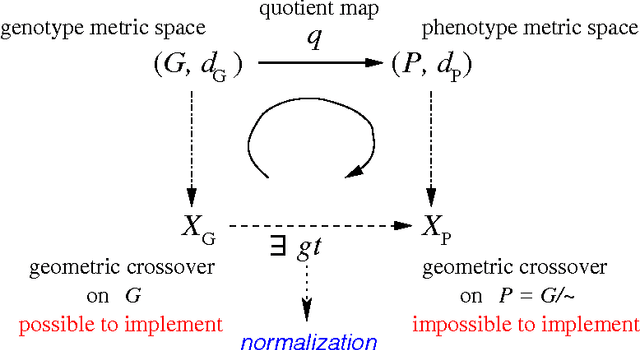
Geometric crossover is a representation-independent definition of crossover based on the distance of the search space interpreted as a metric space. It generalizes the traditional crossover for binary strings and other important recombination operators for the most frequently used representations. Using a distance tailored to the problem at hand, the abstract definition of crossover can be used to design new problem specific crossovers that embed problem knowledge in the search. This paper is motivated by the fact that genotype-phenotype mapping can be theoretically interpreted using the concept of quotient space in mathematics. In this paper, we study a metric transformation, the quotient metric space, that gives rise to the notion of quotient geometric crossover. This turns out to be a very versatile notion. We give many example applications of the quotient geometric crossover.