Charge Scheduling of an Energy Storage System under Time-of-use Pricing and a Demand Charge

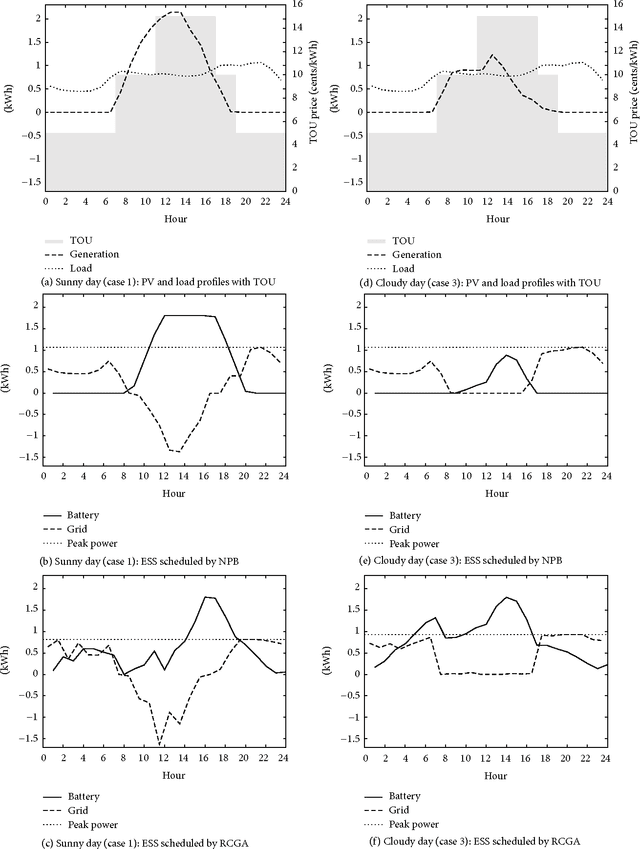
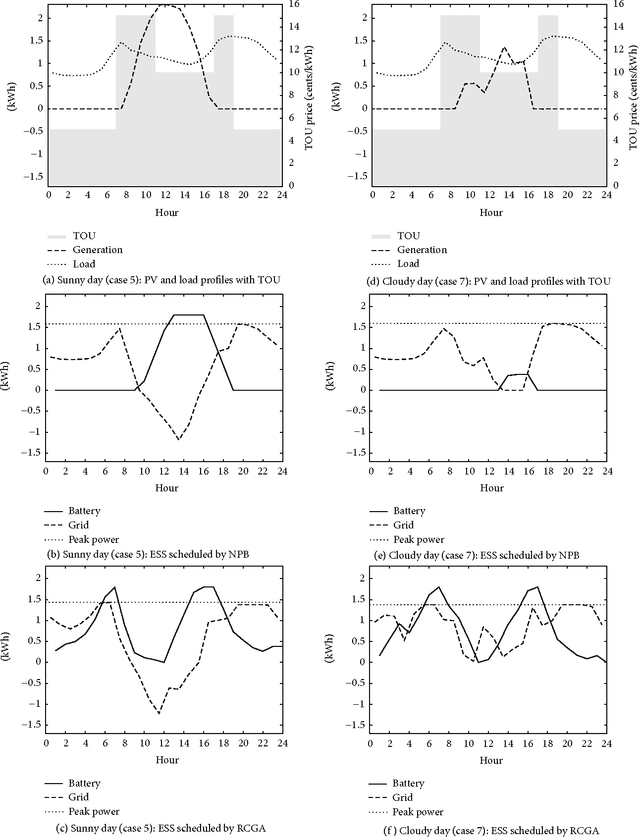
A real-coded genetic algorithm is used to schedule the charging of an energy storage system (ESS), operated in tandem with renewable power by an electricity consumer who is subject to time-of-use pricing and a demand charge. Simulations based on load and generation profiles of typical residential customers show that an ESS scheduled by our algorithm can reduce electricity costs by approximately 17%, compared to a system without an ESS, and by 8% compared to a scheduling algorithm based on net power.

Mathematical Interpretation between Genotype and Phenotype Spaces and Induced Geometric Crossovers

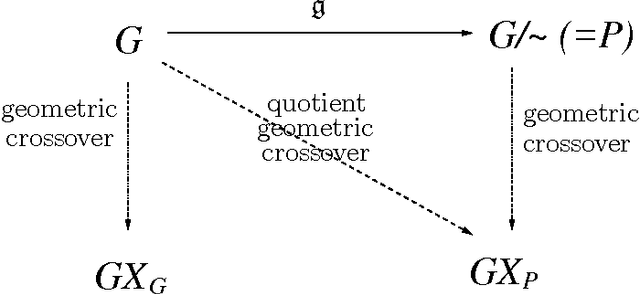
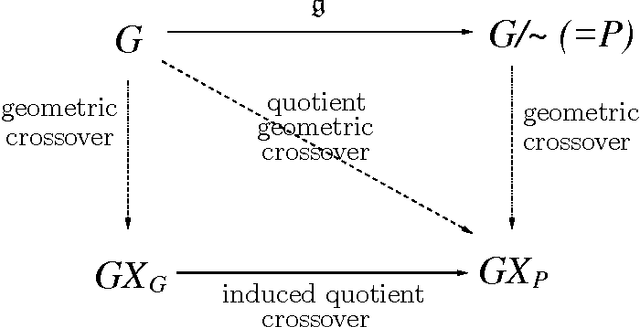
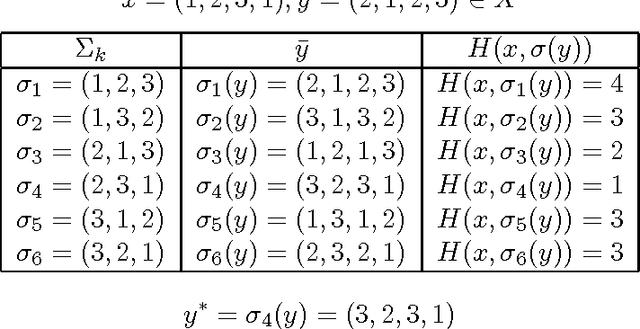
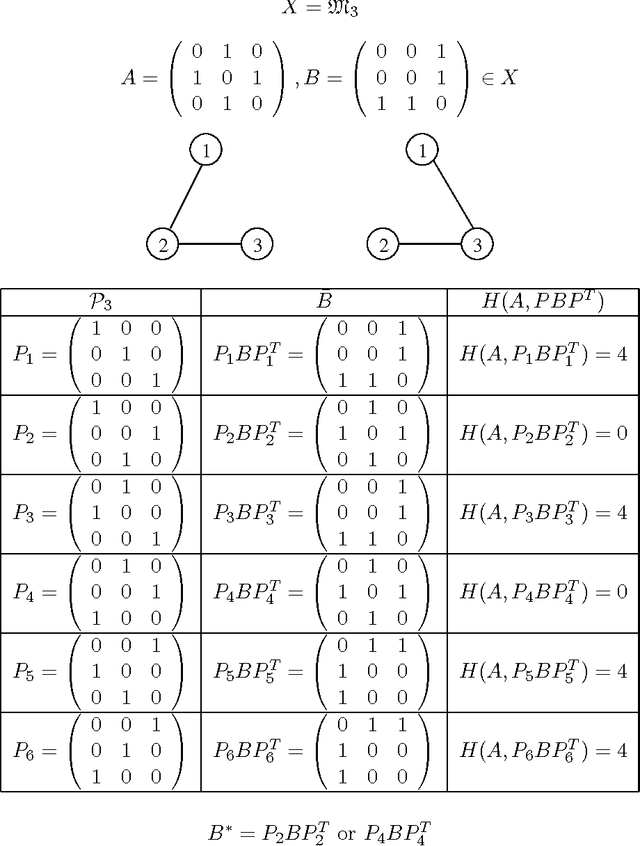
In this paper, we present that genotype-phenotype mapping can be theoretically interpreted using the concept of quotient space in mathematics. Quotient space can be considered as mathematically-defined phenotype space in the evolutionary computation theory. The quotient geometric crossover has the effect of reducing the search space actually searched by geometric crossover, and it introduces problem knowledge in the search by using a distance better tailored to the specific solution interpretation. Quotient geometric crossovers are directly applied to the genotype space but they have the effect of the crossovers performed on phenotype space. We give many example applications of the quotient geometric crossover.

A Mathematical Unification of Geometric Crossovers Defined on Phenotype Space

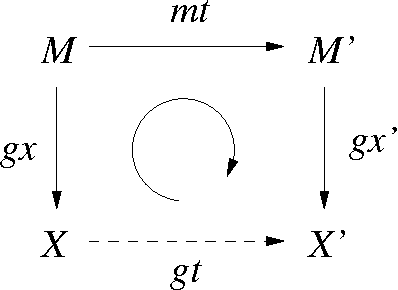
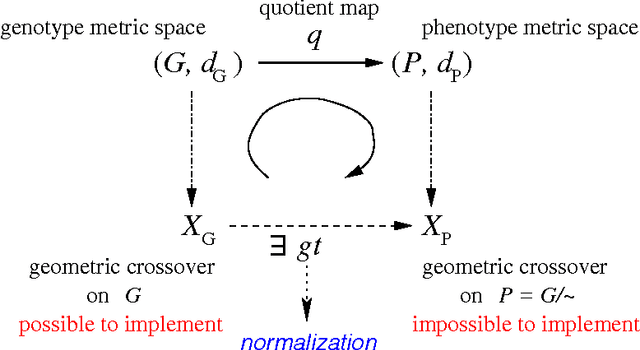
Geometric crossover is a representation-independent definition of crossover based on the distance of the search space interpreted as a metric space. It generalizes the traditional crossover for binary strings and other important recombination operators for the most frequently used representations. Using a distance tailored to the problem at hand, the abstract definition of crossover can be used to design new problem specific crossovers that embed problem knowledge in the search. This paper is motivated by the fact that genotype-phenotype mapping can be theoretically interpreted using the concept of quotient space in mathematics. In this paper, we study a metric transformation, the quotient metric space, that gives rise to the notion of quotient geometric crossover. This turns out to be a very versatile notion. We give many example applications of the quotient geometric crossover.