A Mathematical Unification of Geometric Crossovers Defined on Phenotype Space
Paper and Code
Jul 18, 2009
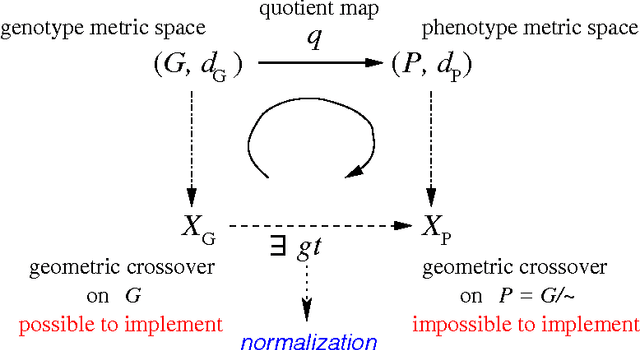
Geometric crossover is a representation-independent definition of crossover based on the distance of the search space interpreted as a metric space. It generalizes the traditional crossover for binary strings and other important recombination operators for the most frequently used representations. Using a distance tailored to the problem at hand, the abstract definition of crossover can be used to design new problem specific crossovers that embed problem knowledge in the search. This paper is motivated by the fact that genotype-phenotype mapping can be theoretically interpreted using the concept of quotient space in mathematics. In this paper, we study a metric transformation, the quotient metric space, that gives rise to the notion of quotient geometric crossover. This turns out to be a very versatile notion. We give many example applications of the quotient geometric crossover.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge