Practical Estimation of Ensemble Accuracy

Ensemble learning combines several individual models to obtain better generalization performance. In this work we present a practical method for estimating the joint power of several classifiers which differs from existing approaches by {\em not relying on labels}, hence enabling the work in unsupervised setting of huge datasets. It differs from existing methods which define a "diversity measure". The heart of the method is a combinatorial bound on the number of mistakes the ensemble is likely to make. The bound can be efficiently approximated in time linear in the number of samples. Thus allowing an efficient search for a combination of classifiers that are likely to produce higher joint accuracy. Moreover, having the bound applicable to unlabeled data makes it both accurate and practical in modern setting of unsupervised learning. We demonstrate the method on popular large-scale face recognition datasets which provide a useful playground for fine-grain classification tasks using noisy data over many classes. The proposed framework fits neatly in trending practices of unsupervised learning. It is a measure of the inherent independence of a set of classifiers not relying on extra information such as another classifier or labeled data.

Learning a Metric Embedding for Face Recognition using the Multibatch Method

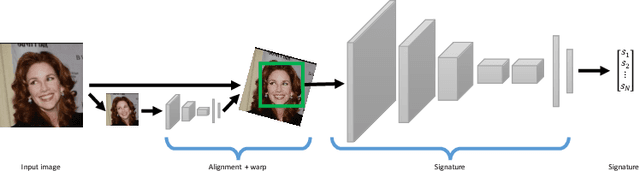
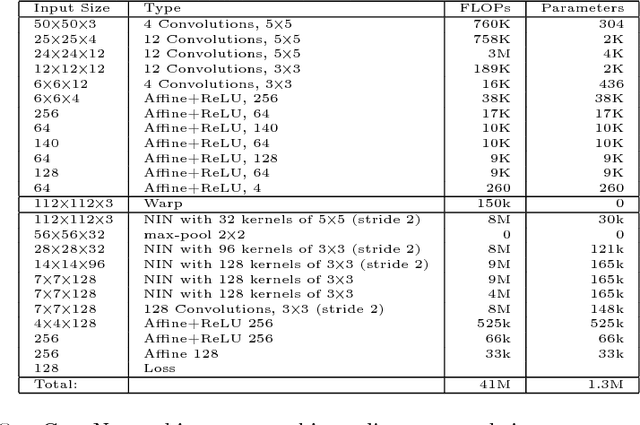
This work is motivated by the engineering task of achieving a near state-of-the-art face recognition on a minimal computing budget running on an embedded system. Our main technical contribution centers around a novel training method, called Multibatch, for similarity learning, i.e., for the task of generating an invariant "face signature" through training pairs of "same" and "not-same" face images. The Multibatch method first generates signatures for a mini-batch of $k$ face images and then constructs an unbiased estimate of the full gradient by relying on all $k^2-k$ pairs from the mini-batch. We prove that the variance of the Multibatch estimator is bounded by $O(1/k^2)$, under some mild conditions. In contrast, the standard gradient estimator that relies on random $k/2$ pairs has a variance of order $1/k$. The smaller variance of the Multibatch estimator significantly speeds up the convergence rate of stochastic gradient descent. Using the Multibatch method we train a deep convolutional neural network that achieves an accuracy of $98.2\%$ on the LFW benchmark, while its prediction runtime takes only $30$msec on a single ARM Cortex A9 core. Furthermore, the entire training process took only 12 hours on a single Titan X GPU.

Minimizing the Maximal Loss: How and Why?

A commonly used learning rule is to approximately minimize the \emph{average} loss over the training set. Other learning algorithms, such as AdaBoost and hard-SVM, aim at minimizing the \emph{maximal} loss over the training set. The average loss is more popular, particularly in deep learning, due to three main reasons. First, it can be conveniently minimized using online algorithms, that process few examples at each iteration. Second, it is often argued that there is no sense to minimize the loss on the training set too much, as it will not be reflected in the generalization loss. Last, the maximal loss is not robust to outliers. In this paper we describe and analyze an algorithm that can convert any online algorithm to a minimizer of the maximal loss. We prove that in some situations better accuracy on the training set is crucial to obtain good performance on unseen examples. Last, we propose robust versions of the approach that can handle outliers.

ShareBoost: Efficient Multiclass Learning with Feature Sharing

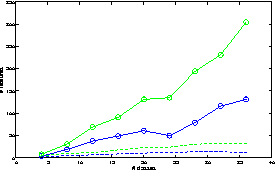
Multiclass prediction is the problem of classifying an object into a relevant target class. We consider the problem of learning a multiclass predictor that uses only few features, and in particular, the number of used features should increase sub-linearly with the number of possible classes. This implies that features should be shared by several classes. We describe and analyze the ShareBoost algorithm for learning a multiclass predictor that uses few shared features. We prove that ShareBoost efficiently finds a predictor that uses few shared features (if such a predictor exists) and that it has a small generalization error. We also describe how to use ShareBoost for learning a non-linear predictor that has a fast evaluation time. In a series of experiments with natural data sets we demonstrate the benefits of ShareBoost and evaluate its success relatively to other state-of-the-art approaches.