Critical Iterative Denoising: A Discrete Generative Model Applied to Graphs

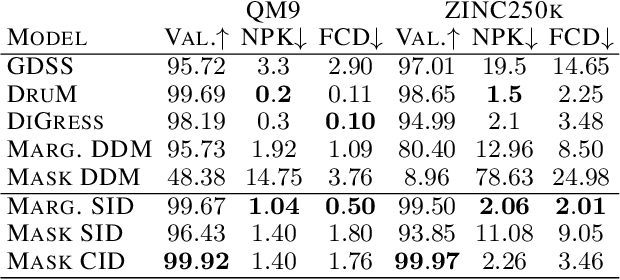
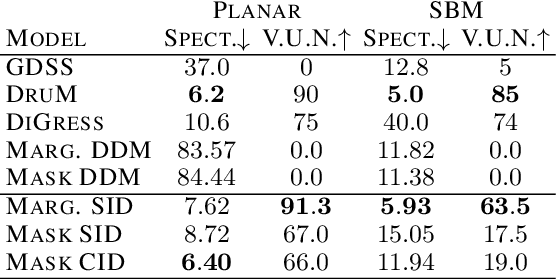
Discrete Diffusion and Flow Matching models have significantly advanced generative modeling for discrete structures, including graphs. However, the time dependencies in the noising process of these models lead to error accumulation and propagation during the backward process. This issue, particularly pronounced in mask diffusion, is a known limitation in sequence modeling and, as we demonstrate, also impacts discrete diffusion models for graphs. To address this problem, we propose a novel framework called Iterative Denoising, which simplifies discrete diffusion and circumvents the issue by assuming conditional independence across time. Additionally, we enhance our model by incorporating a Critic, which during generation selectively retains or corrupts elements in an instance based on their likelihood under the data distribution. Our empirical evaluations demonstrate that the proposed method significantly outperforms existing discrete diffusion baselines in graph generation tasks.

Discrete Latent Graph Generative Modeling with Diffusion Bridges

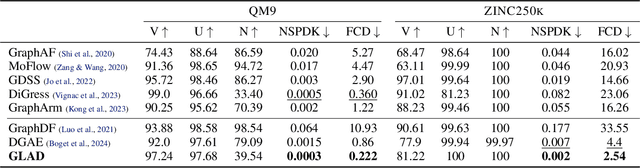
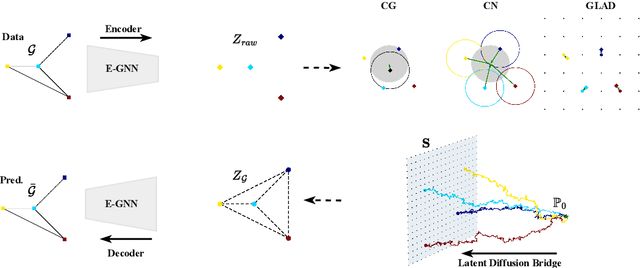
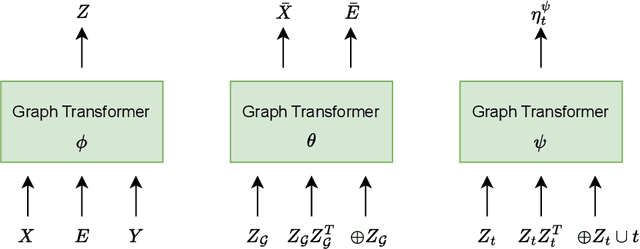
Learning graph generative models over latent spaces has received less attention compared to models that operate on the original data space and has so far demonstrated lacklustre performance. We present GLAD a latent space graph generative model. Unlike most previous latent space graph generative models, GLAD operates on a discrete latent space that preserves to a significant extent the discrete nature of the graph structures making no unnatural assumptions such as latent space continuity. We learn the prior of our discrete latent space by adapting diffusion bridges to its structure. By operating over an appropriately constructed latent space we avoid relying on decompositions that are often used in models that operate in the original data space. We present experiments on a series of graph benchmark datasets which clearly show the superiority of the discrete latent space and obtain state of the art graph generative performance, making GLAD the first latent space graph generative model with competitive performance. Our source code is published at: \url{https://github.com/v18nguye/GLAD}.

Vector-Quantized Graph Auto-Encoder

In this work, we addresses the problem of modeling distributions of graphs. We introduce the Vector-Quantized Graph Auto-Encoder (VQ-GAE), a permutation-equivariant discrete auto-encoder and designed to model the distribution of graphs. By exploiting the permutation-equivariance of graph neural networks (GNNs), our autoencoder circumvents the problem of the ordering of the graph representation. We leverage the capability of GNNs to capture local structures of graphs while employing vector-quantization to prevent the mapping of discrete objects to a continuous latent space. Furthermore, the use of autoregressive models enables us to capture the global structure of graphs via the latent representation. We evaluate our model on standard datasets used for graph generation and observe that it achieves excellent performance on some of the most salient evaluation metrics compared to the state-of-the-art.

GrannGAN: Graph annotation generative adversarial networks

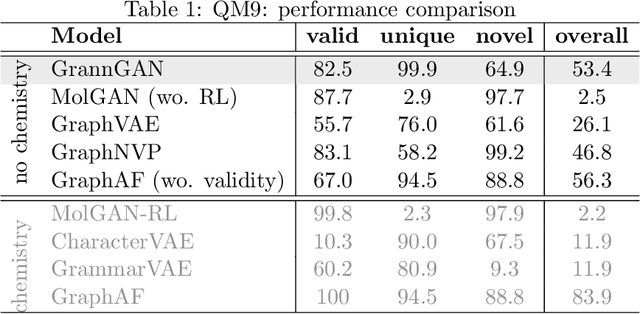
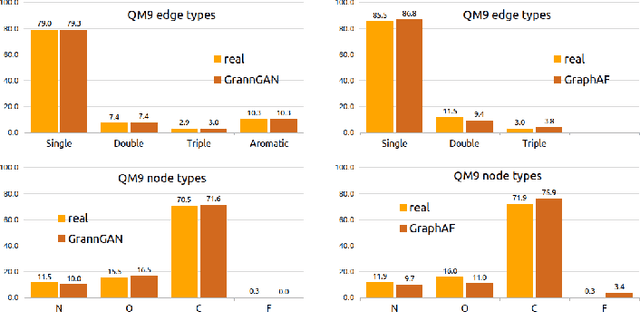
We consider the problem of modelling high-dimensional distributions and generating new examples of data with complex relational feature structure coherent with a graph skeleton. The model we propose tackles the problem of generating the data features constrained by the specific graph structure of each data point by splitting the task into two phases. In the first it models the distribution of features associated with the nodes of the given graph, in the second it complements the edge features conditionally on the node features. We follow the strategy of implicit distribution modelling via generative adversarial network (GAN) combined with permutation equivariant message passing architecture operating over the sets of nodes and edges. This enables generating the feature vectors of all the graph objects in one go (in 2 phases) as opposed to a much slower one-by-one generations of sequential models, prevents the need for expensive graph matching procedures usually needed for likelihood-based generative models, and uses efficiently the network capacity by being insensitive to the particular node ordering in the graph representation. To the best of our knowledge, this is the first method that models the feature distribution along the graph skeleton allowing for generations of annotated graphs with user specified structures. Our experiments demonstrate the ability of our model to learn complex structured distributions through quantitative evaluation over three annotated graph datasets.

Permutation Equivariant Generative Adversarial Networks for Graphs

One of the most discussed issues in graph generative modeling is the ordering of the representation. One solution consists of using equivariant generative functions, which ensure the ordering invariance. After having discussed some properties of such functions, we propose 3G-GAN, a 3-stages model relying on GANs and equivariant functions. The model is still under development. However, we present some encouraging exploratory experiments and discuss the issues still to be addressed.

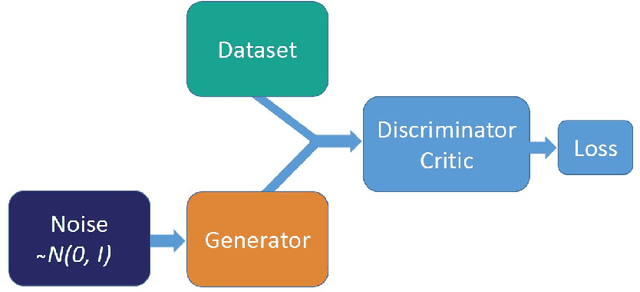
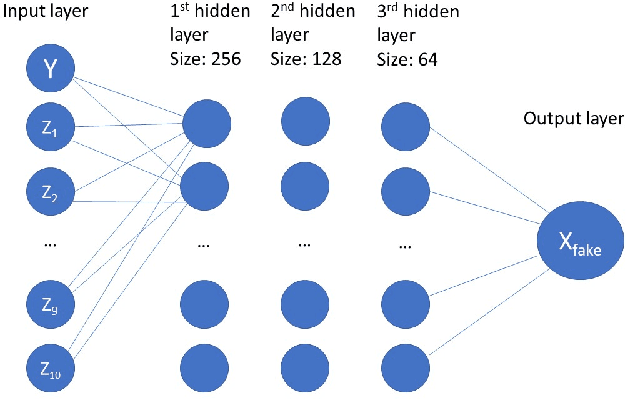
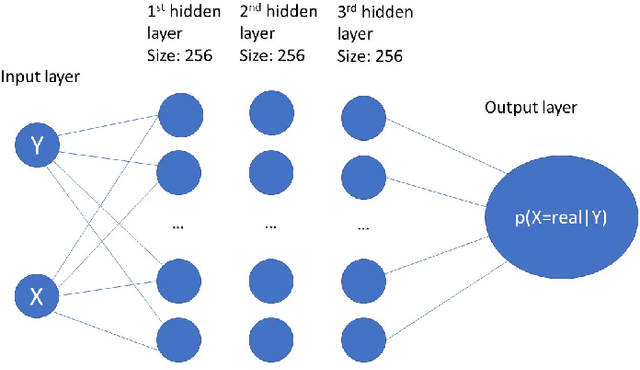
Adversarial Regression. Generative Adversarial Networks for Non-Linear Regression: Theory and Assessment

Adversarial Regression is a proposition to perform high dimensional non-linear regression with uncertainty estimation. We used Conditional Generative Adversarial Network to obtain an estimate of the full predictive distribution for a new observation. Generative Adversarial Networks (GAN) are implicit generative models which produce samples from a distribution approximating the distribution of the data. The conditional version of it (CGAN) takes the following expression: $\min\limits_G \max\limits_D V(D, G) = \mathbb{E}_{x\sim p_{r}(x)} [log(D(x, y))] + \mathbb{E}_{z\sim p_{z}(z)} [log (1-D(G(z, y)))]$. An approximate solution can be found by training simultaneously two neural networks to model D and G and feeding G with a random noise vector $z$. After training, we have that $G(z, y)\mathrel{\dot\sim} p_{data}(x, y)$. By fixing $y$, we have $G(z|y) \mathrel{\dot\sim} p{data}(x|y)$. By sampling $z$, we can therefore obtain samples following approximately $p(x|y)$, which is the predictive distribution of $x$ for a new $y$. We ran experiments to test various loss functions, data distributions, sample size, size of the noise vector, etc. Even if we observed differences, no experiment outperformed consistently the others. The quality of CGAN for regression relies on fine-tuning a range of hyperparameters. In a broader view, the results show that CGANs are very promising methods to perform uncertainty estimation for high dimensional non-linear regression.