Sliced-Wasserstein Distribution Alignment Loss Improves the Ultra-Low-Bit Quantization of Large Language Models

The benefits of most large language models come with steep and often hidden economic and environmental costs due to their resource usage inefficiency during deployment. Model quantization improves energy and memory efficiency through representing model parameters by lower-precision values. However, compression below 4-bits often distorts activation distributions and degrades performance. We address this challenge by introducing a sliced Wasserstein loss function for distribution-aware calibration in ultra-low-bit post-training quantization. The proposed loss aligns the output distributions of full-precision and quantized models under random linear projections, complementing standard mean-squared error loss without adding any computational overhead during inference. Our proposed loss function can be incorporated with any post-training quantization framework that has a retraining component. We demonstrate the performance gains of our proposed model by incorporating it with two frontier methods known as OmniQuant and TesseraQ. Compared to these two baselines, the proposed loss consistently improves both perplexity and downstream task accuracy across multiple ultra-low-bit settings. Our proposed loss function recovers 4.12-20.37% of the OmniQuant's lost accuracy on the language model LLaMA-2-7B, 0.93-7.65% on OPT-6.7B, and 2.26-6.20% on LLaMA-2-13B. TesseraQ's accuracy degradation is recovered by 3.63-7.63% in relative terms when augmented by our proposed loss function. Taken together, these results demonstrate that distributional alignment provides a simple yet effective performance boost that can push the limits of frontier quantization methods. Our method is available on GitHub to facilitate future progress in ultra-low-bit quantization.

Composite Adaptive Control for Bilateral Teleoperation Systems without Persistency of Excitation

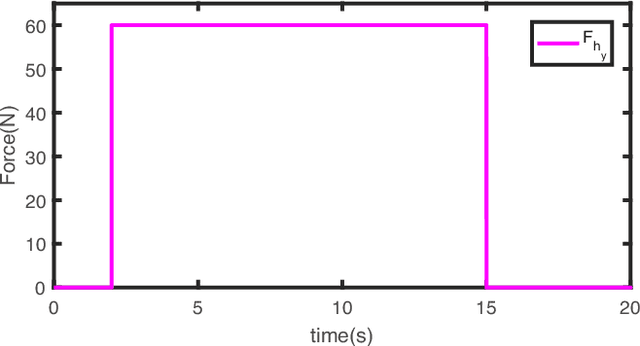
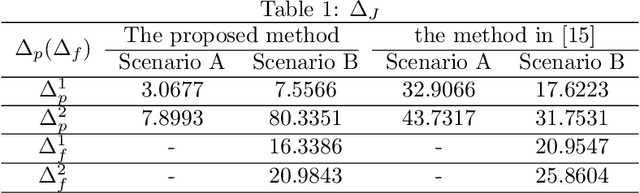
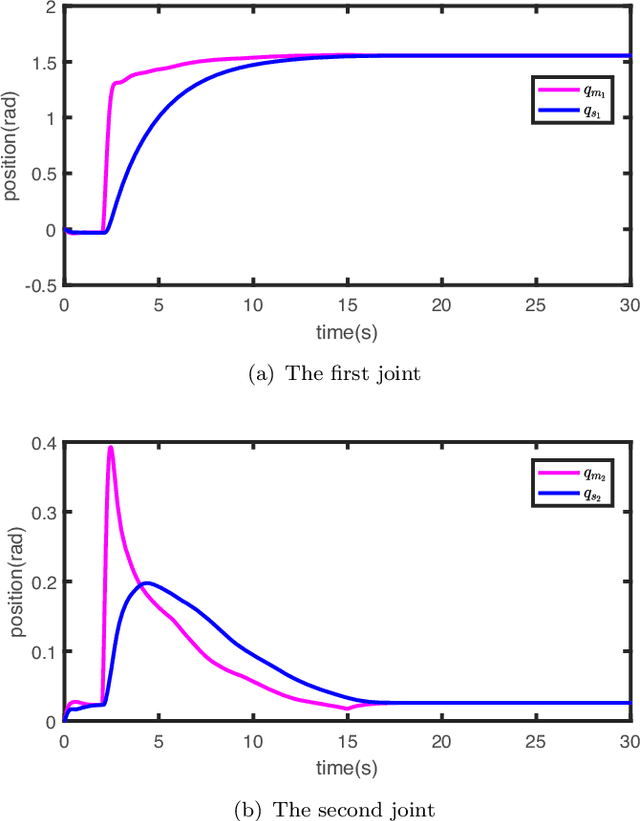
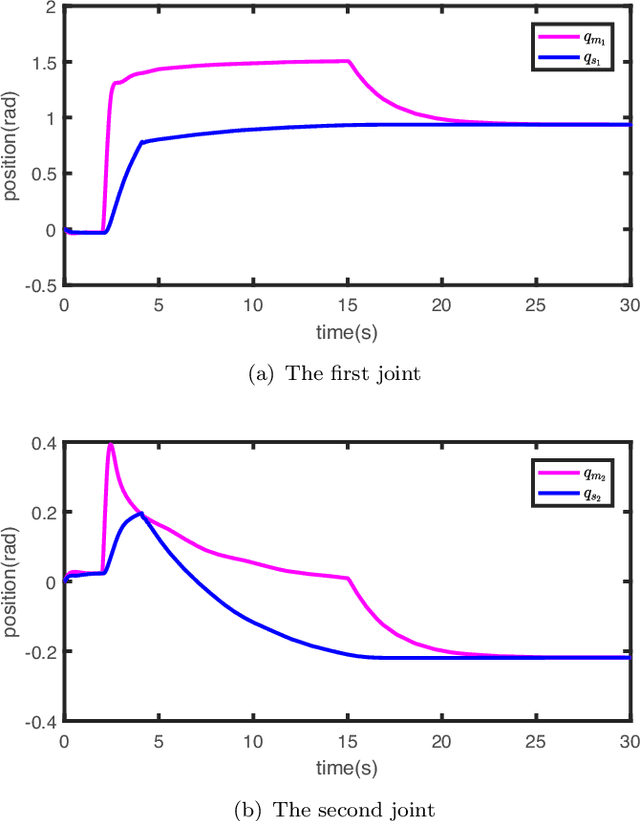
Composite adaptive control schemes, which use both the system tracking errors and the prediction error to drive the update laws, have become widespread in achieving an improvement of system performance. However, a strong persistent-excitation (PE) condition should be satisfied to guarantee the parameter convergence. This paper proposes a novel composite adaptive control to guarantee parameter convergence without PE condition for nonlinear teleoperation systems with dynamic uncertainties and time-varying communication delays. The stability criteria of the closed-loop teleoperation system are given in terms of linear matrix inequalities. New tracking performance measures are proposed to evaluate the position tracking between the master and the slave. Simulation studies are given to show the effectiveness of the proposed method.