Removing grid structure in angle-resolved photoemission spectra via deep learning method

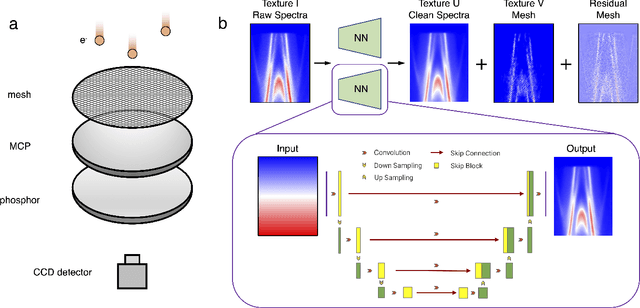
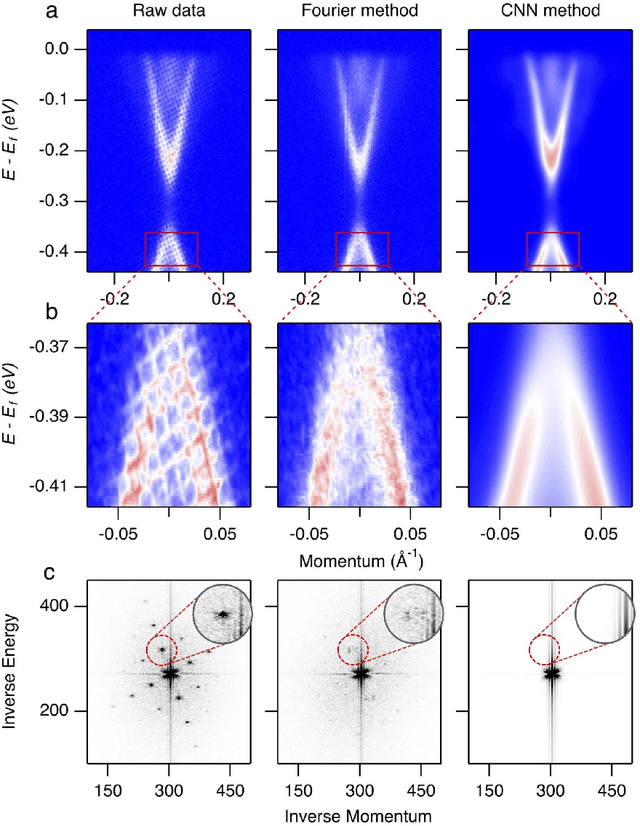
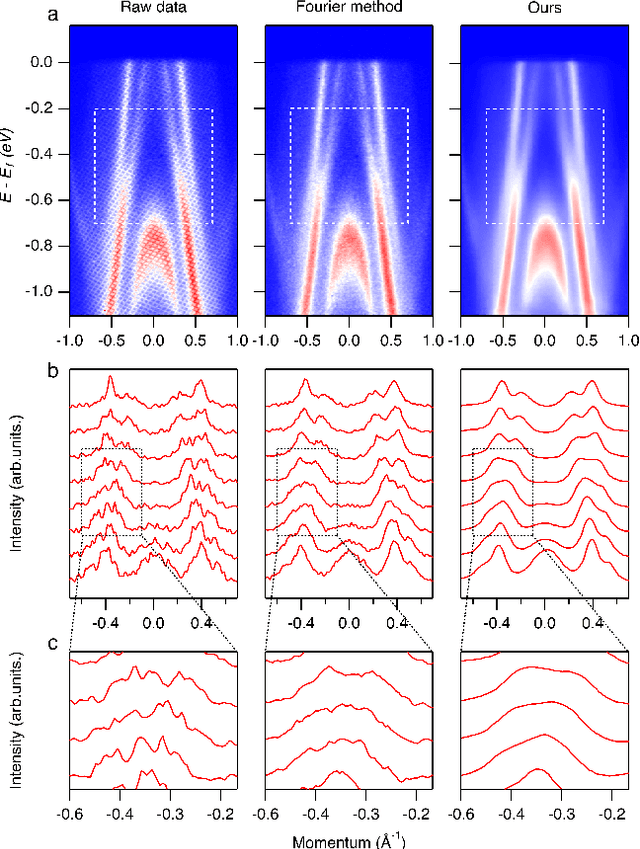
Spectroscopic data may often contain unwanted extrinsic signals. For example, in ARPES experiment, a wire mesh is typically placed in front of the CCD to block stray photo-electrons, but could cause a grid-like structure in the spectra during quick measurement mode. In the past, this structure was often removed using the mathematical Fourier filtering method by erasing the periodic structure. However, this method may lead to information loss and vacancies in the spectra because the grid structure is not strictly linearly superimposed. Here, we propose a deep learning method to effectively overcome this problem. Our method takes advantage of the self-correlation information within the spectra themselves and can greatly optimize the quality of the spectra while removing the grid structure and noise simultaneously. It has the potential to be extended to all spectroscopic measurements to eliminate other extrinsic signals and enhance the spectral quality based on the self-correlation of the spectra solely.

Spectroscopic data de-noising via training-set-free deep learning method

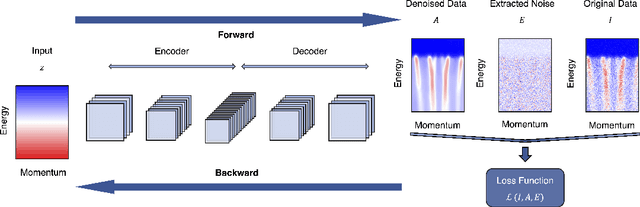
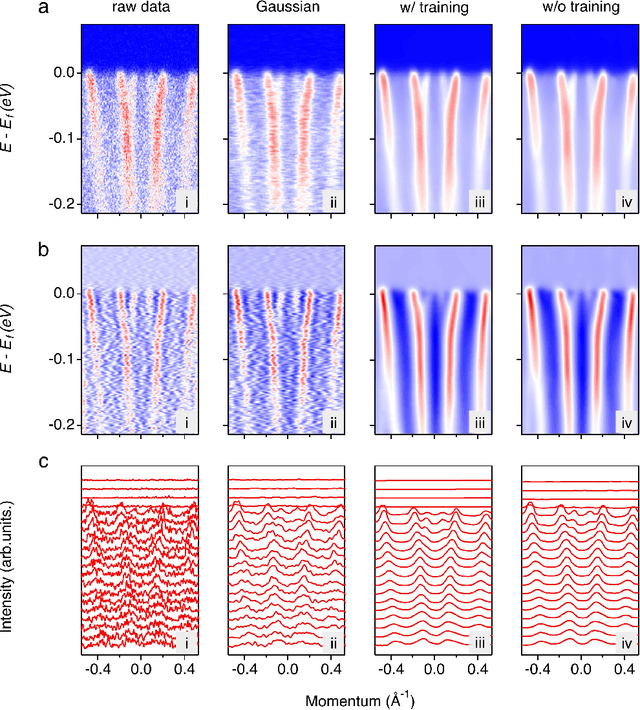
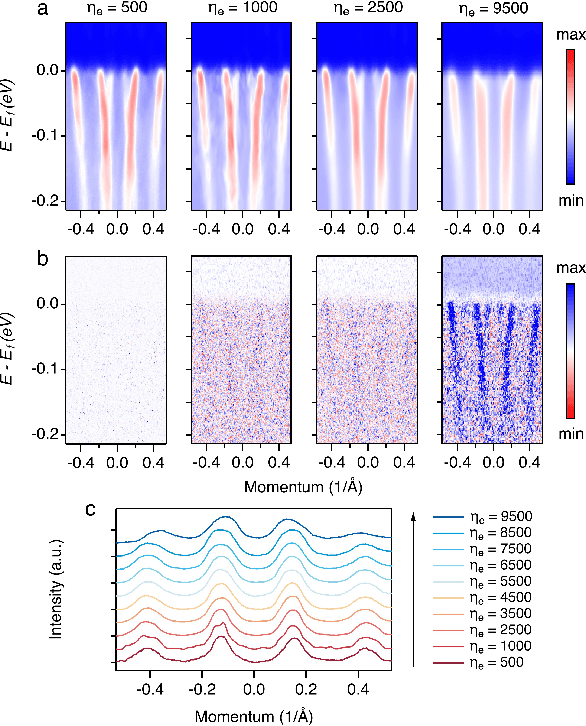
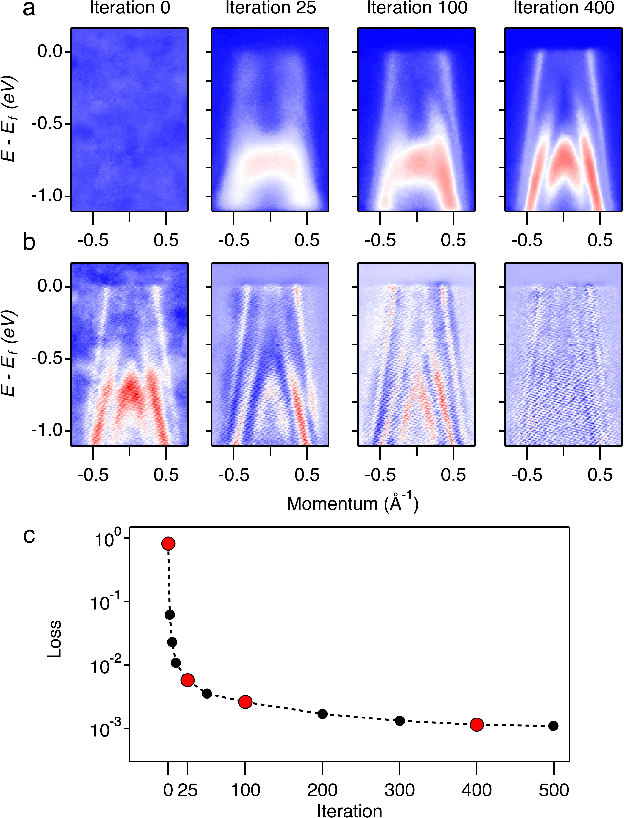
De-noising plays a crucial role in the post-processing of spectra. Machine learning-based methods show good performance in extracting intrinsic information from noisy data, but often require a high-quality training set that is typically inaccessible in real experimental measurements. Here, using spectra in angle-resolved photoemission spectroscopy (ARPES) as an example, we develop a de-noising method for extracting intrinsic spectral information without the need for a training set. This is possible as our method leverages the self-correlation information of the spectra themselves. It preserves the intrinsic energy band features and thus facilitates further analysis and processing. Moreover, since our method is not limited by specific properties of the training set compared to previous ones, it may well be extended to other fields and application scenarios where obtaining high-quality multidimensional training data is challenging.

Learned Optimizers for Analytic Continuation

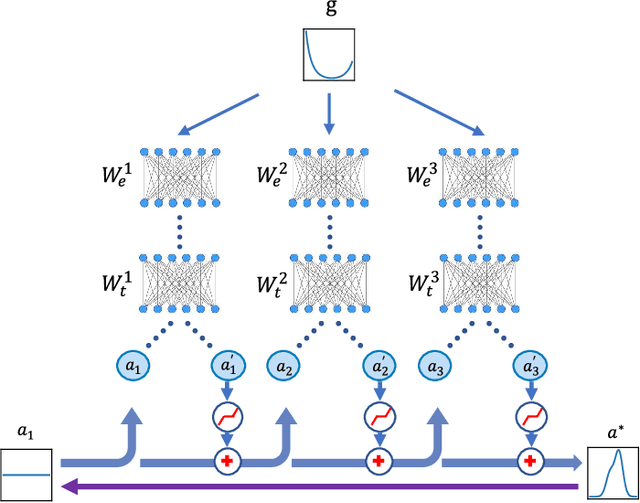
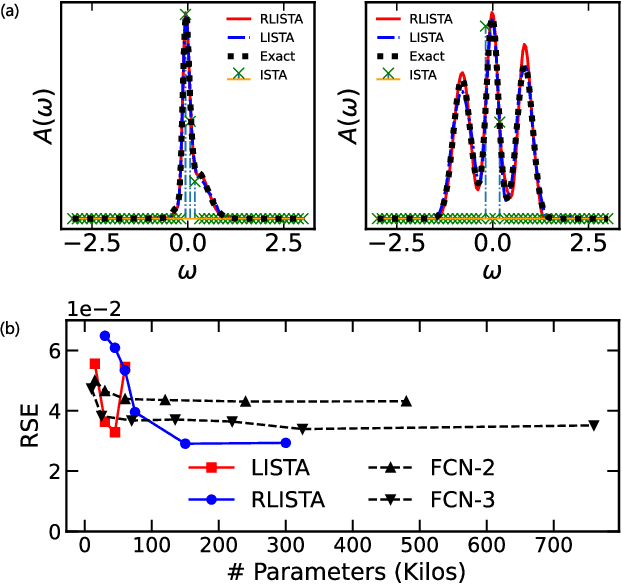
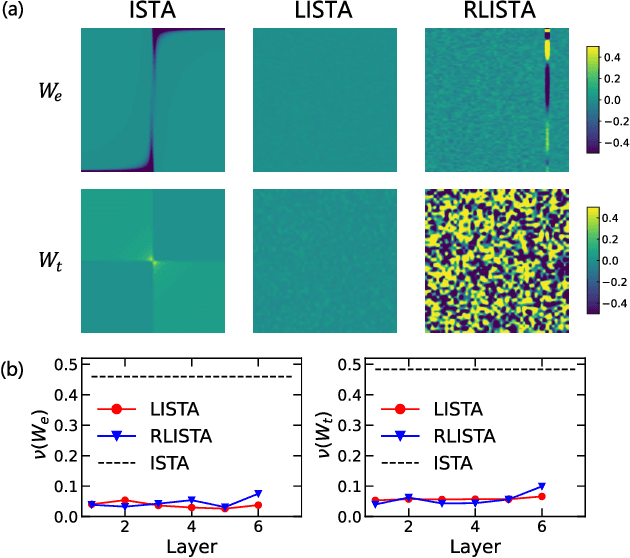
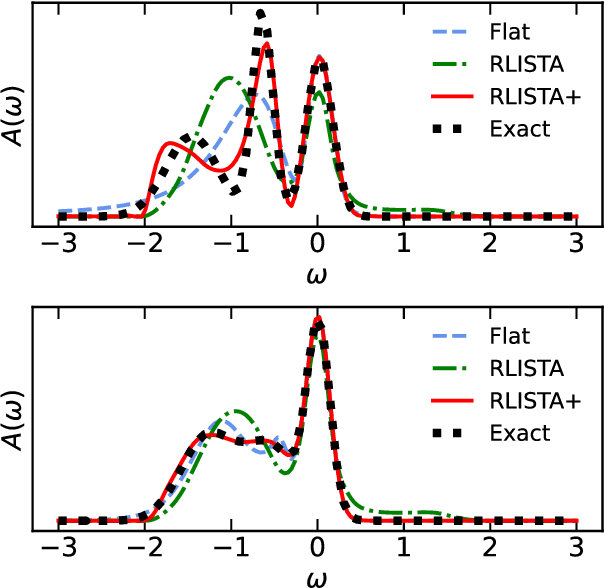
Traditional maximum entropy and sparsity-based algorithms for analytic continuation often suffer from the ill-posed kernel matrix or demand tremendous computation time for parameter tuning. Here we propose a neural network method by convex optimization and replace the ill-posed inverse problem by a sequence of well-conditioned surrogate problems. After training, the learned optimizers are able to give a solution of high quality with low time cost and achieve higher parameter efficiency than heuristic full-connected networks. The output can also be used as a neural default model to improve the maximum entropy for better performance. Our methods may be easily extended to other high-dimensional inverse problems via large-scale pretraining.

Recommender Engine for Continuous Time Quantum Monte Carlo Methods

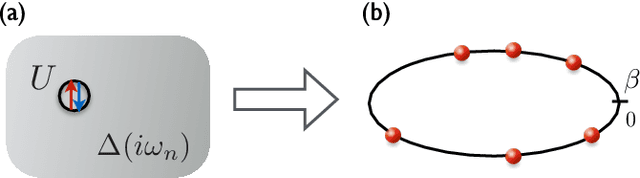
Recommender systems play an essential role in the modern business world. They recommend favorable items like books, movies, and search queries to users based on their past preferences. Applying similar ideas and techniques to Monte Carlo simulations of physical systems boosts their efficiency without sacrificing accuracy. Exploiting the quantum to classical mapping inherent in the continuous-time quantum Monte Carlo methods, we construct a classical molecular gas model to reproduce the quantum distributions. We then utilize powerful molecular simulation techniques to propose efficient quantum Monte Carlo updates. The recommender engine approach provides a general way to speed up the quantum impurity solvers.