Training-set-free two-stage deep learning for spectroscopic data de-noising

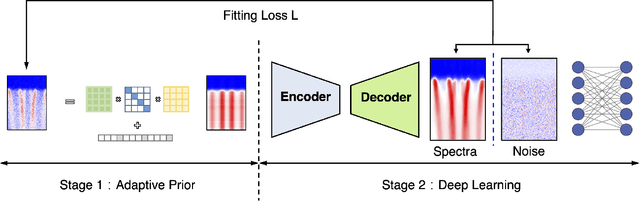
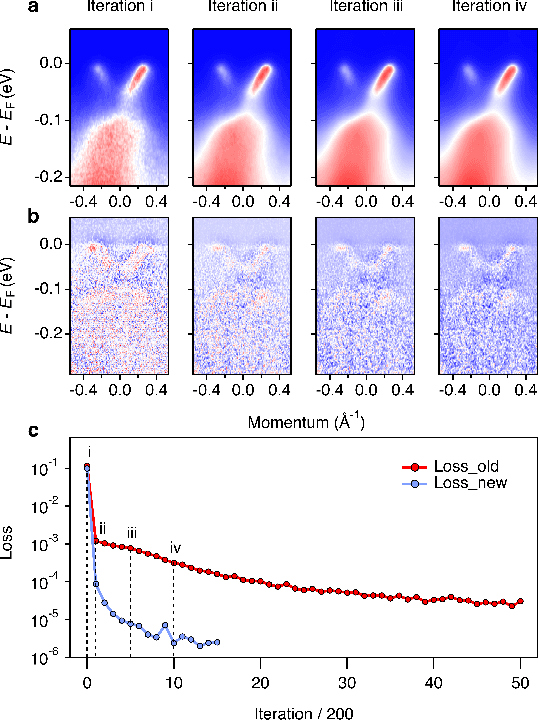
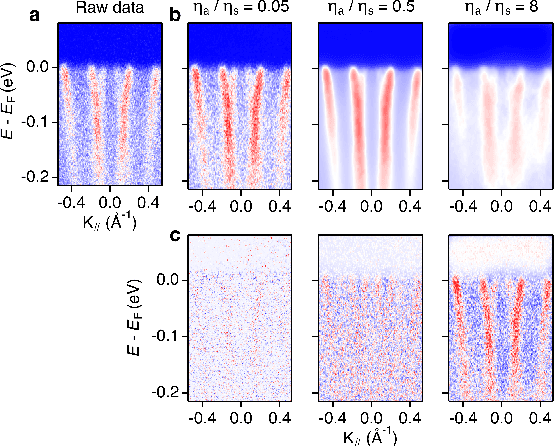
De-noising is a prominent step in the spectra post-processing procedure. Previous machine learning-based methods are fast but mostly based on supervised learning and require a training set that may be typically expensive in real experimental measurements. Unsupervised learning-based algorithms are slow and require many iterations to achieve convergence. Here, we bridge this gap by proposing a training-set-free two-stage deep learning method. We show that the fuzzy fixed input in previous methods can be improved by introducing an adaptive prior. Combined with more advanced optimization techniques, our approach can achieve five times acceleration compared to previous work. Theoretically, we study the landscape of a corresponding non-convex linear problem, and our results indicates that this problem has benign geometry for first-order algorithms to converge.

Removing grid structure in angle-resolved photoemission spectra via deep learning method

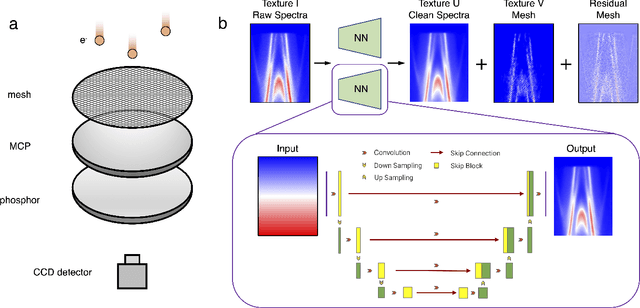
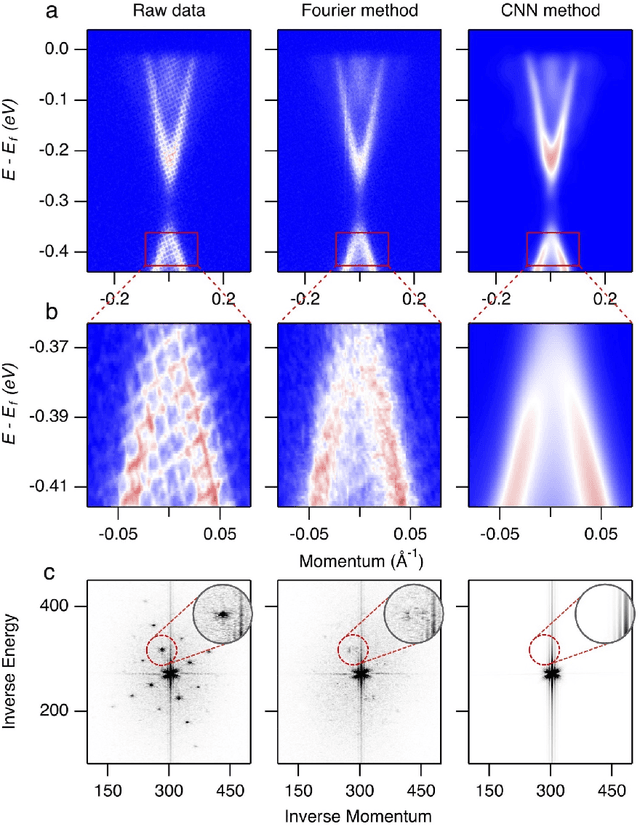
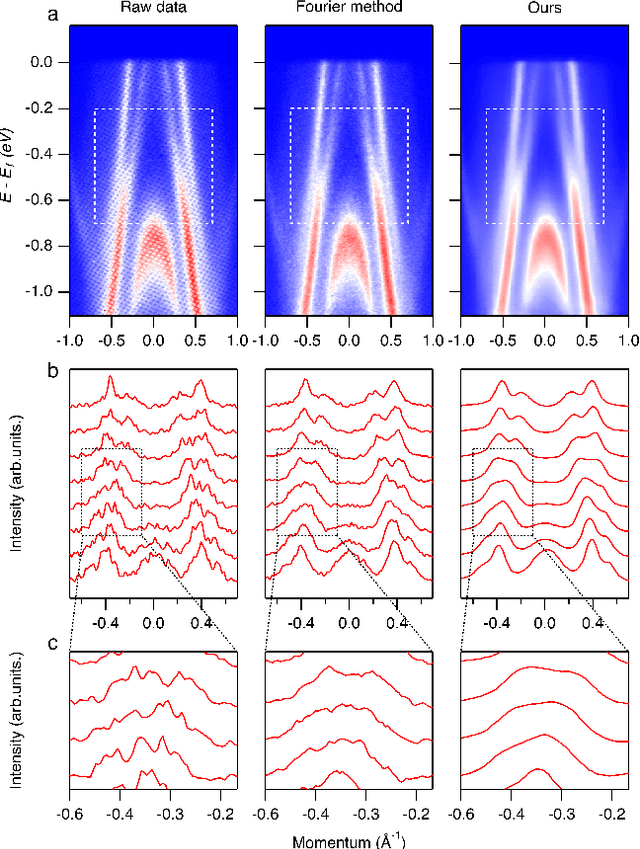
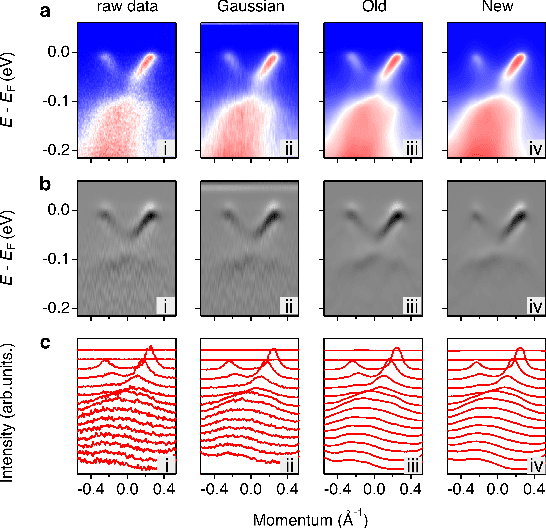
Spectroscopic data may often contain unwanted extrinsic signals. For example, in ARPES experiment, a wire mesh is typically placed in front of the CCD to block stray photo-electrons, but could cause a grid-like structure in the spectra during quick measurement mode. In the past, this structure was often removed using the mathematical Fourier filtering method by erasing the periodic structure. However, this method may lead to information loss and vacancies in the spectra because the grid structure is not strictly linearly superimposed. Here, we propose a deep learning method to effectively overcome this problem. Our method takes advantage of the self-correlation information within the spectra themselves and can greatly optimize the quality of the spectra while removing the grid structure and noise simultaneously. It has the potential to be extended to all spectroscopic measurements to eliminate other extrinsic signals and enhance the spectral quality based on the self-correlation of the spectra solely.

Spectroscopic data de-noising via training-set-free deep learning method

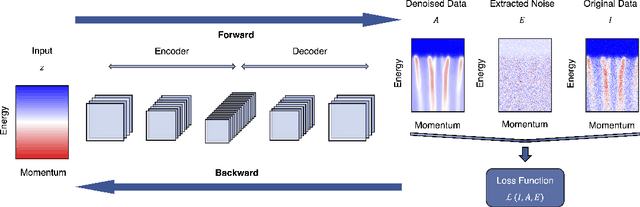
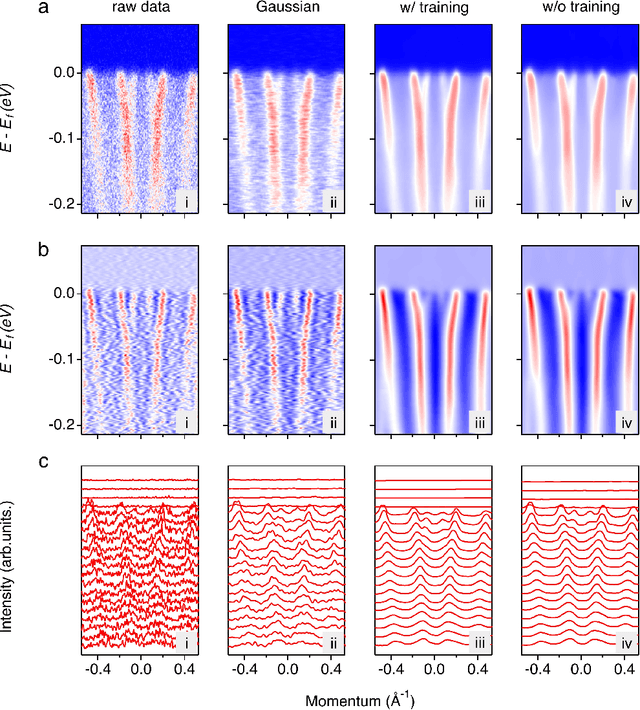
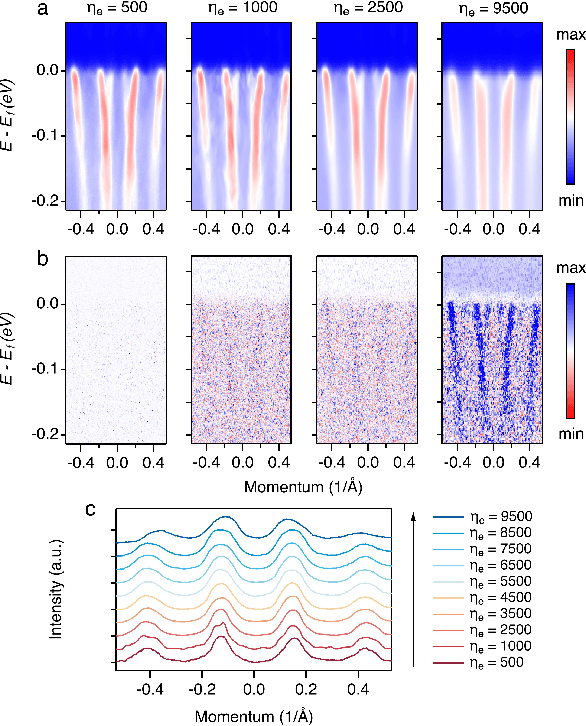
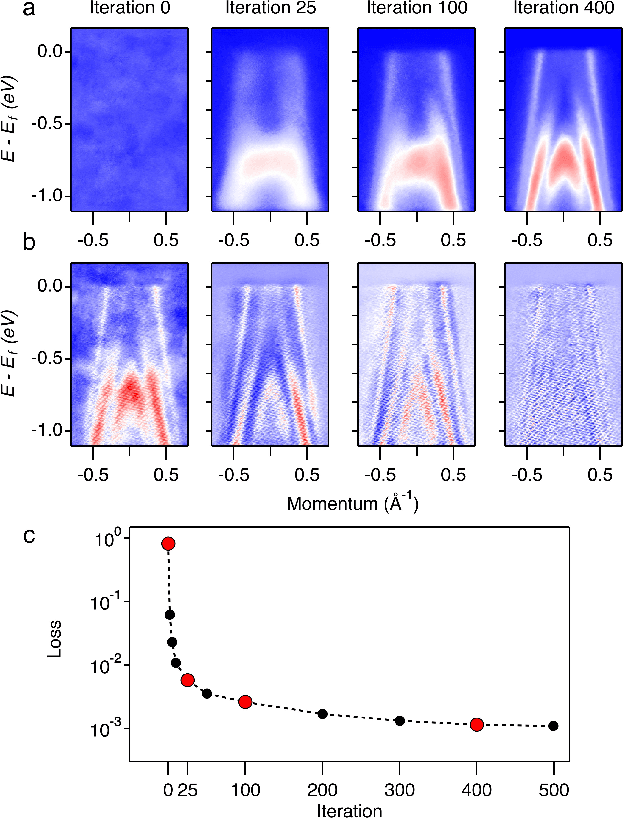
De-noising plays a crucial role in the post-processing of spectra. Machine learning-based methods show good performance in extracting intrinsic information from noisy data, but often require a high-quality training set that is typically inaccessible in real experimental measurements. Here, using spectra in angle-resolved photoemission spectroscopy (ARPES) as an example, we develop a de-noising method for extracting intrinsic spectral information without the need for a training set. This is possible as our method leverages the self-correlation information of the spectra themselves. It preserves the intrinsic energy band features and thus facilitates further analysis and processing. Moreover, since our method is not limited by specific properties of the training set compared to previous ones, it may well be extended to other fields and application scenarios where obtaining high-quality multidimensional training data is challenging.