Compressed BC-LISTA via Low-Rank Convolutional Decomposition

We study Sparse Signal Recovery (SSR) methods for multichannel imaging with compressed {forward and backward} operators that preserve reconstruction accuracy. We propose a Compressed Block-Convolutional (C-BC) measurement model based on a low-rank Convolutional Neural Network (CNN) decomposition that is analytically initialized from a low-rank factorization of physics-derived forward/backward operators in time delay-based measurements. We use Orthogonal Matching Pursuit (OMP) to select a compact set of basis filters from the analytic model and compute linear mixing coefficients to approximate the full model. We consider the Learned Iterative Shrinkage-Thresholding Algorithm (LISTA) network as a representative example for which the C-BC-LISTA extension is presented. In simulated multichannel ultrasound imaging across multiple Signal-to-Noise Ratios (SNRs), C-BC-LISTA requires substantially fewer parameters and smaller model size than other state-of-the-art (SOTA) methods while improving reconstruction accuracy. In ablations over OMP, Singular Value Decomposition (SVD)-based, and random initializations, OMP-initialized structured compression performs best, yielding the most efficient training and the best performance.

Plug-and-Play Latent Diffusion for Electromagnetic Inverse Scattering with Application to Brain Imaging

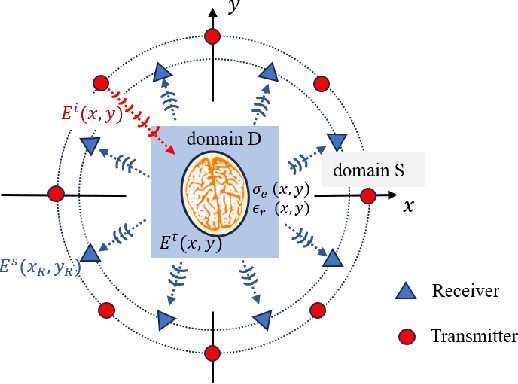
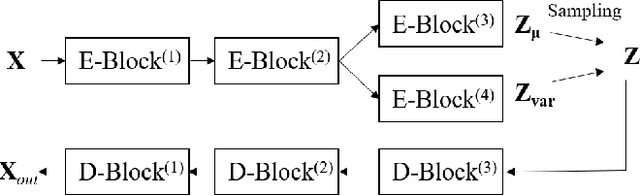
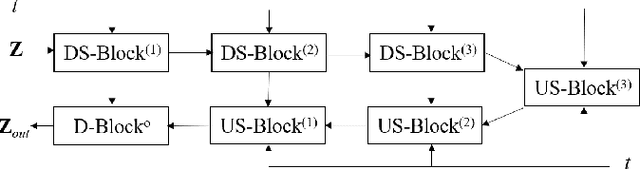
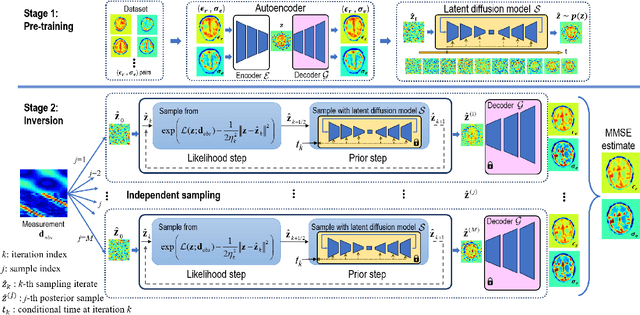
Electromagnetic (EM) imaging is an important tool for non-invasive sensing with low-cost and portable devices. One emerging application is EM stroke imaging, which enables early diagnosis and continuous monitoring of brain strokes. Quantitative imaging is achieved by solving an inverse scattering problem (ISP) that reconstructs permittivity and conductivity maps from measurements. In general, the reconstruction accuracy is limited by its inherent nonlinearity and ill-posedness. Existing methods, including learning-free and learning-based approaches, fail to either incorporate complicated prior distributions or provide theoretical guarantees, posing difficulties in balancing interpretability, distortion error, and reliability. To overcome these limitations, we propose a posterior sampling method based on latent diffusion for quantitative EM brain imaging, adapted from a generative plug-and-play (PnP) posterior sampling framework. Our approach allows to flexibly integrate prior knowledge into physics-based inversion without requiring paired measurement-label datasets. We first learn the prior distribution of targets from an unlabeled dataset, and then incorporate the learned prior into posterior sampling. In particular, we train a latent diffusion model on permittivity and conductivity maps to capture their prior distribution. Then, given measurements and the forward model describing EM wave physics, we perform posterior sampling by alternating between two samplers that respectively enforce the likelihood and prior distributions. Finally, reliable reconstruction is obtained through minimum mean squared error (MMSE) estimation based on the samples. Experimental results on brain imaging demonstrate that our approach achieves state-of-the-art performance in reconstruction accuracy and structural similarity while maintaining high measurement fidelity.

Practical Modulo Sampling: Mitigating High-Frequency Components

Recovering signals within limited dynamic range (DR) constraints remains a central challenge for analog-to-digital converters (ADCs). To prevent data loss, an ADCs DR typically must exceed that of the input signal. Modulo sampling has recently gained attention as a promising approach for addressing DR limitations across various signal classes. However, existing methods often rely on ideal ADCs capable of capturing the high frequencies introduced by the modulo operator, which is impractical in real-world hardware applications. This paper introduces an innovative hardware-based sampling approach that addresses these high-frequency components using an analog mixer followed by a Low-Pass Filter (LPF). This allows the use of realistic ADCs, which do not need to handle frequencies beyond the intended sampling rate. Our method eliminates the requirement for high-specification ADCs and demonstrates that the resulting samples are equivalent to those from an ideal high-spec ADC. Consequently, any existing modulo recovery algorithm can be applied effectively. We present a practical hardware prototype of this approach, validated through both simulations and hardware recovery experiments. Using a recovery method designed to handle quantization noise, we show that our approach effectively manages high-frequency artifacts, enabling reliable modulo recovery with realistic ADCs. These findings confirm that our hardware solution not only outperforms conventional methods in high-precision settings but also demonstrates significant real-world applicability.

Modulo Sampling in Shift-Invariant Spaces: Recovery and Stability Enhancement

Sampling shift-invariant (SI) signals with a high dynamic range poses a notable challenge in the domain of analog-to-digital conversion (ADC). It is essential for the ADC's dynamic range to exceed that of the incoming analog signal to ensure no vital information is lost during the conversion process. Modulo sampling, an approach initially explored with bandlimited (BL) signals, offers a promising solution to overcome the constraints of dynamic range. In this paper, we expand on the recent advancements in modulo sampling to encompass a broader range of SI signals. Our proposed strategy incorporates analog preprocessing, including the use of a mixer and a low-pass filter (LPF), to transform the signal into a bandlimited one. This BL signal can be accurately reconstructed from its modulo samples if sampled at slightly above its Nyquist frequency. The recovery of the original SI signal from this BL representation is then achieved through suitable filtering. We also examine the efficacy of this system across various noise conditions. Careful choice of the mixer plays a pivotal role in enhancing the method's reliability, especially with generators prone to instability. Our approach thus broadens the framework of modulo sampling's utility in efficiently recovering SI signals, pushing its boundaries beyond BL signals while sampling only slightly above the rate needed for a SI signal.

Efficient Convolutional Forward Modeling and Sparse Coding in Multichannel Imaging

This study considers the Block-Toeplitz structural properties inherent in traditional multichannel forward model matrices, using Full Matrix Capture (FMC) in ultrasonic testing as a case study. We propose an analytical convolutional forward model that transforms reflectivity maps into FMC data. Our findings demonstrate that the convolutional model excels over its matrix-based counterpart in terms of computational efficiency and storage requirements. This accelerated forward modeling approach holds significant potential for various inverse problems, notably enhancing Sparse Signal Recovery (SSR) within the context LASSO regression, which facilitates efficient Convolutional Sparse Coding (CSC) algorithms. Additionally, we explore the integration of Convolutional Neural Networks (CNNs) for the forward model, employing deep unfolding to implement the Learned Block Convolutional ISTA (BC-LISTA).