Push--Pull with Device Sampling

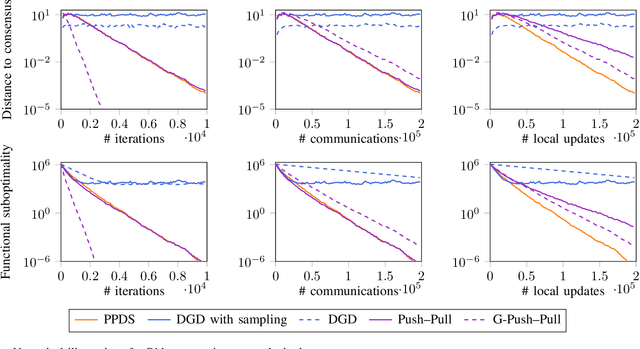
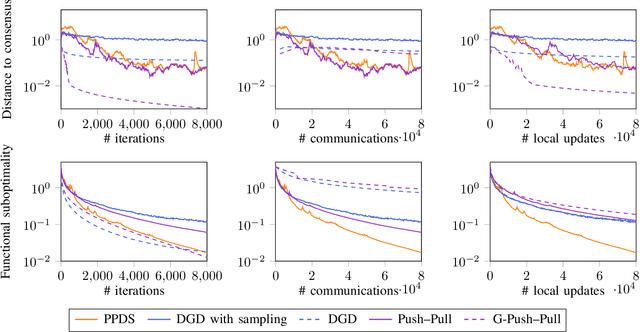
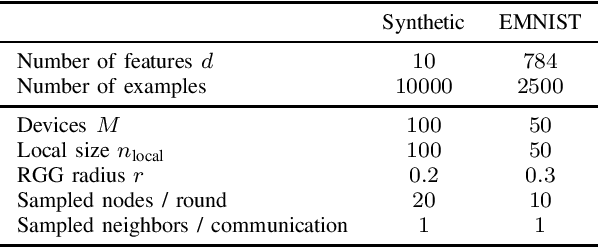
We consider decentralized optimization problems in which a number of agents collaborate to minimize the average of their local functions by exchanging over an underlying communication graph. Specifically, we place ourselves in an asynchronous model where only a random portion of nodes perform computation at each iteration, while the information exchange can be conducted between all the nodes and in an asymmetric fashion. For this setting, we propose an algorithm that combines gradient tracking and variance reduction over the entire network. This enables each node to track the average of the gradients of the objective functions. Our theoretical analysis shows that the algorithm converges linearly, when the local objective functions are strongly convex, under mild connectivity conditions on the expected mixing matrices. In particular, our result does not require the mixing matrices to be doubly stochastic. In the experiments, we investigate a broadcast mechanism that transmits information from computing nodes to their neighbors, and confirm the linear convergence of our method on both synthetic and real-world datasets.

Federated Learning with Heterogeneous Data: A Superquantile Optimization Approach

We present a federated learning framework that is designed to robustly deliver good predictive performance across individual clients with heterogeneous data. The proposed approach hinges upon a superquantile-based learning objective that captures the tail statistics of the error distribution over heterogeneous clients. We present a stochastic training algorithm which interleaves differentially private client reweighting steps with federated averaging steps. The proposed algorithm is supported with finite time convergence guarantees that cover both convex and non-convex settings. Experimental results on benchmark datasets for federated learning demonstrate that our approach is competitive with classical ones in terms of average error and outperforms them in terms of tail statistics of the error.

First-order Optimization for Superquantile-based Supervised Learning

Classical supervised learning via empirical risk (or negative log-likelihood) minimization hinges upon the assumption that the testing distribution coincides with the training distribution. This assumption can be challenged in modern applications of machine learning in which learning machines may operate at prediction time with testing data whose distribution departs from the one of the training data. We revisit the superquantile regression method by proposing a first-order optimization algorithm to minimize a superquantile-based learning objective. The proposed algorithm is based on smoothing the superquantile function by infimal convolution. Promising numerical results illustrate the interest of the approach towards safer supervised learning.

Device Heterogeneity in Federated Learning: A Superquantile Approach

We propose a federated learning framework to handle heterogeneous client devices which do not conform to the population data distribution. The approach hinges upon a parameterized superquantile-based objective, where the parameter ranges over levels of conformity. We present an optimization algorithm and establish its convergence to a stationary point. We show how to practically implement it using secure aggregation by interleaving iterations of the usual federated averaging method with device filtering. We conclude with numerical experiments on neural networks as well as linear models on tasks from computer vision and natural language processing.