PhysGNN: A Physics-Driven Graph Neural Network Based Model for Predicting Soft Tissue Deformation in Image-Guided Neurosurgery

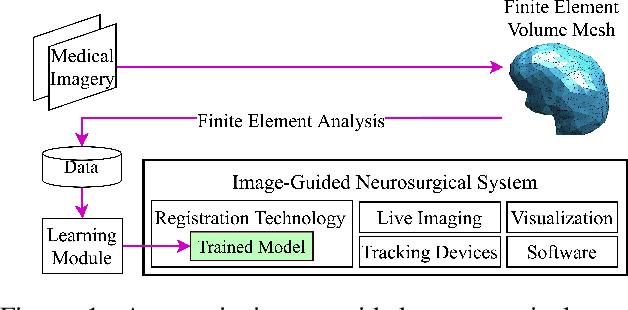
Correctly capturing intraoperative brain shift in image-guided neurosurgical procedures is a critical task for aligning preoperative data with intraoperative geometry, ensuring effective surgical navigation and optimal surgical precision. While the finite element method (FEM) is a proven technique to effectively approximate soft tissue deformation through biomechanical formulations, their degree of success boils down to a trade-off between accuracy and speed. To circumvent this problem, the most recent works in this domain have proposed leveraging data-driven models obtained by training various machine learning algorithms, e.g. random forests, artificial neural networks (ANNs), with the results of finite element analysis (FEA) to speed up tissue deformation approximations by prediction. These methods, however, do not account for the structure of the finite element (FE) mesh during training that provides information on node connectivities as well as the distance between them, which can aid with approximating tissue deformation based on the proximity of force load points with the rest of the mesh nodes. Therefore, this work proposes a novel framework, PhysGNN, a data-driven model that approximates the solution of FEA by leveraging graph neural networks (GNNs), which are capable of accounting for the mesh structural information and inductive learning over unstructured grids and complex topological structures. Empirically, we demonstrate that the proposed architecture, PhysGNN, promises accurate and fast soft tissue deformation approximations while remaining computationally feasible, suitable for neurosurgical settings.

Structure Aware Negative Sampling in Knowledge Graphs

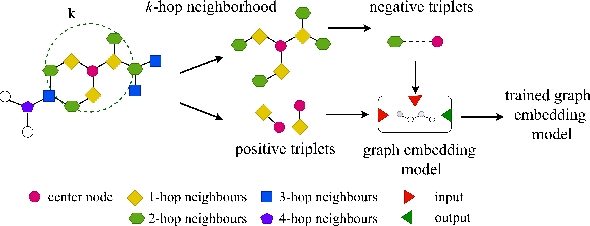
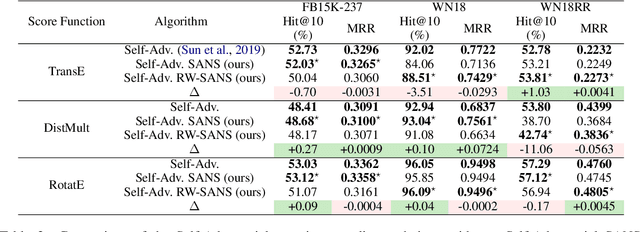
Learning low-dimensional representations for entities and relations in knowledge graphs using contrastive estimation represents a scalable and effective method for inferring connectivity patterns. A crucial aspect of contrastive learning approaches is the choice of corruption distribution that generates hard negative samples, which force the embedding model to learn discriminative representations and find critical characteristics of observed data. While earlier methods either employ too simple corruption distributions, i.e. uniform, yielding easy uninformative negatives or sophisticated adversarial distributions with challenging optimization schemes, they do not explicitly incorporate known graph structure resulting in suboptimal negatives. In this paper, we propose Structure Aware Negative Sampling (SANS), an inexpensive negative sampling strategy that utilizes the rich graph structure by selecting negative samples from a node's k-hop neighborhood. Empirically, we demonstrate that SANS finds semantically meaningful negatives and is competitive with SOTA approaches while requires no additional parameters nor difficult adversarial optimization.