Beyond the density operator and Tr: Exploiting the higher-order statistics of random-coefficient pure states for quantum information processing

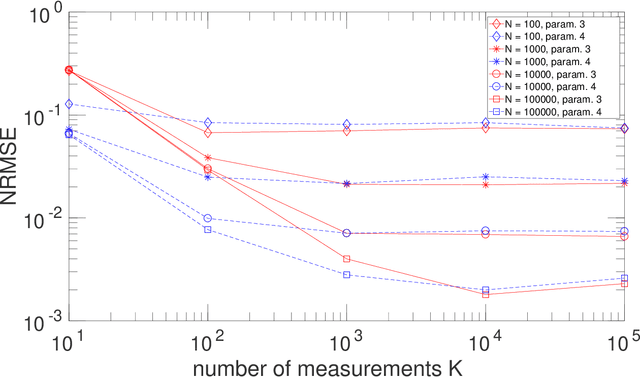
Two types of states are widely used in quantum mechanics, namely (deterministic-coefficient) pure states and statistical mixtures. A density operator can be associated with each of them. We here address a third type of states, that we previously introduced in a more restricted framework. These states generalize pure ones by replacing each of their deterministic ket coefficients by a random variable. We therefore call them Random-Coefficient Pure States, or RCPS. We analyze their properties and their relationships with both types of usual states. We show that RCPS contain much richer information than the density operator and mean of observables that we associate with them. This occurs because the latter operator only exploits the second-order statistics of the random state coefficients, whereas their higher-order statistics contain additional information. That information can be accessed in practice with the multiple-preparation procedure that we propose for RCPS, by using second-order and higher-order statistics of associated random probabilities of measurement outcomes. Exploiting these higher-order statistics opens the way to a very general approach for performing advanced quantum information processing tasks. We illustrate the relevance of this approach with a generic example, dealing with the estimation of parameters of a quantum process and thus related to quantum process tomography. This parameter estimation is performed in the non-blind (i.e. supervised) or blind (i.e. unsupervised) mode. We show that this problem cannot be solved by using only the density operator \rho of an RCPS and the associated mean value Tr(\rho A) of the operator A that corresponds to the considered physical quantity. We succeed in solving this problem by exploiting a fourth-order statistical parameter of state coefficients, in addition to second-order statistics. Numerical tests validate this result.

Single-preparation unsupervised quantum machine learning: concepts and applications

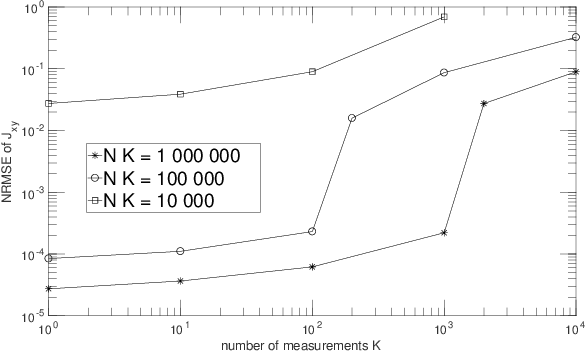
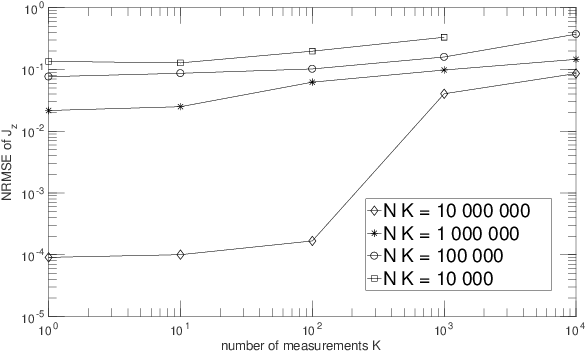
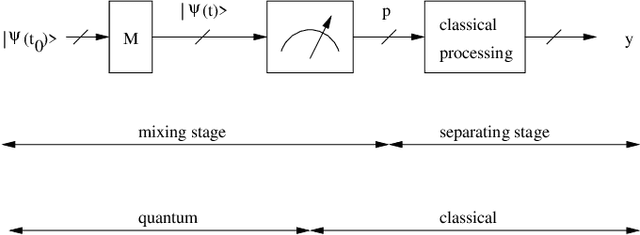
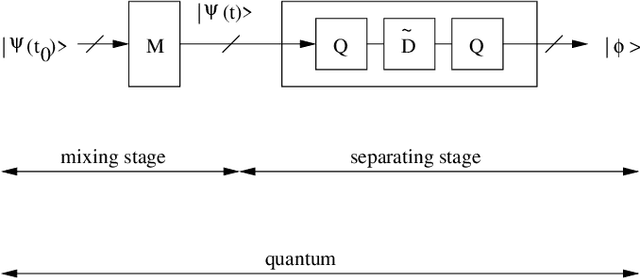
The term "machine learning" especially refers to algorithms that derive mappings, i.e. intput/output transforms, by using numerical data that provide information about considered transforms. These transforms appear in many problems, related to classification/clustering, regression, system identification, system inversion and input signal restoration/separation. We here first analyze the connections between all these problems, in the classical and quantum frameworks. We then focus on their most challenging versions, involving quantum data and/or quantum processing means, and unsupervised, i.e. blind, learning. Moreover, we propose the quite general concept of SIngle-Preparation Quantum Information Processing (SIPQIP). The resulting methods only require a single instance of each state, whereas usual methods have to very accurately create many copies of each fixed state. We apply our SIPQIP concept to various tasks, related to system identification (blind quantum process tomography or BQPT, blind Hamiltonian parameter estimation or BHPE, blind quantum channel identification/estimation, blind phase estimation), system inversion and state estimation (blind quantum source separation or BQSS, blind quantum entangled state restoration or BQSR, blind quantum channel equalization) and classification. Numerical tests show that our framework moreover yields much more accurate estimation than the standard multiple-preparation approach. Our methods are especially useful in a quantum computer, that we propose to more briefly call a "quamputer": BQPT and BHPE simplify the characterization of the gates of quamputers; BQSS and BQSR allow one to design quantum gates that may be used to compensate for the non-idealities that alter states stored in quantum registers, and they open the way to the much more general concept of self-adaptive quantum gates (see longer version of abstract in paper).

Quantum process tomography with unknown single-preparation input states

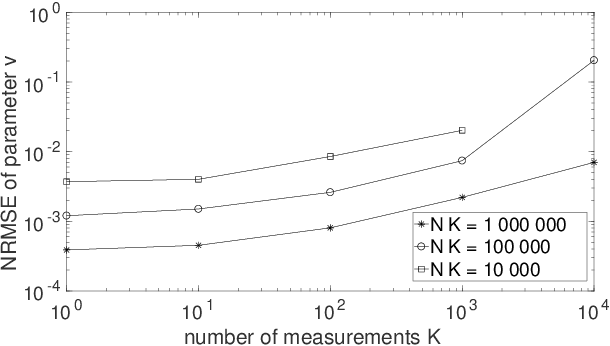
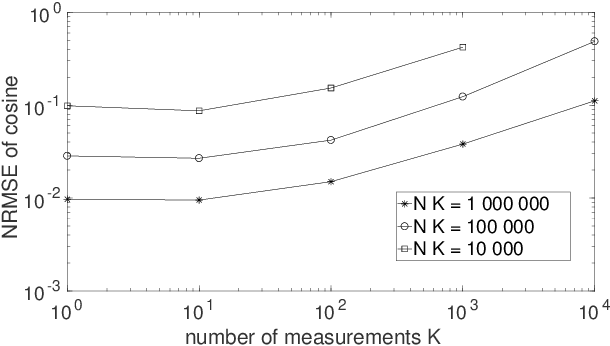
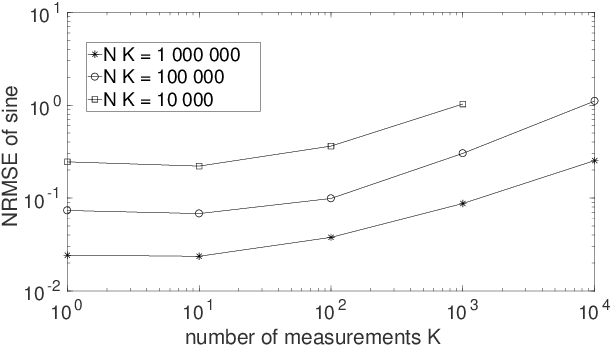
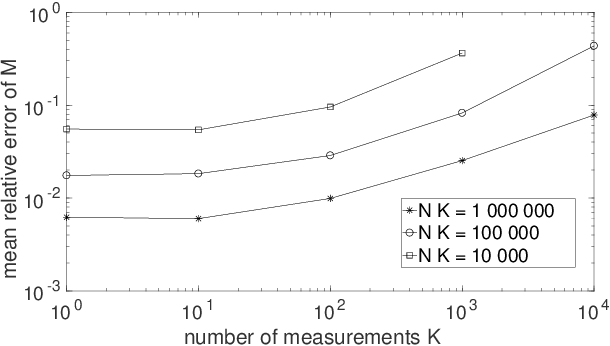
Quantum Process Tomography (QPT) methods aim at identifying, i.e. estimating, a given quantum process. QPT is a major quantum information processing tool, since it especially allows one to characterize the actual behavior of quantum gates, which are the building blocks of quantum computers. However, usual QPT procedures are complicated, since they set several constraints on the quantum states used as inputs of the process to be characterized. In this paper, we extend QPT so as to avoid two such constraints. On the one hand, usual QPT methods requires one to know, hence to precisely control (i.e. prepare), the specific quantum states used as inputs of the considered quantum process, which is cumbersome. We therefore propose a Blind, or unsupervised, extension of QPT (i.e. BQPT), which means that this approach uses input quantum states whose values are unknown and arbitrary, except that they are requested to meet some general known properties (and this approach exploits the output states of the considered quantum process). On the other hand, usual QPT methods require one to be able to prepare many copies of the same (known) input state, which is constraining. On the contrary, we propose "single-preparation methods", i.e. methods which can operate with only one instance of each considered input state. These two new concepts are here illustrated with practical BQPT methods which are numerically validated, in the case when: i) random pure states are used as inputs and their required properties are especially related to the statistical independence of the random variables that define them, ii) the considered quantum process is based on cylindrical-symmetry Heisenberg spin coupling. These concepts may be extended to a much wider class of processes and to BQPT methods based on other input quantum state properties.

Inertia-Constrained Pixel-by-Pixel Nonnegative Matrix Factorisation: a Hyperspectral Unmixing Method Dealing with Intra-class Variability

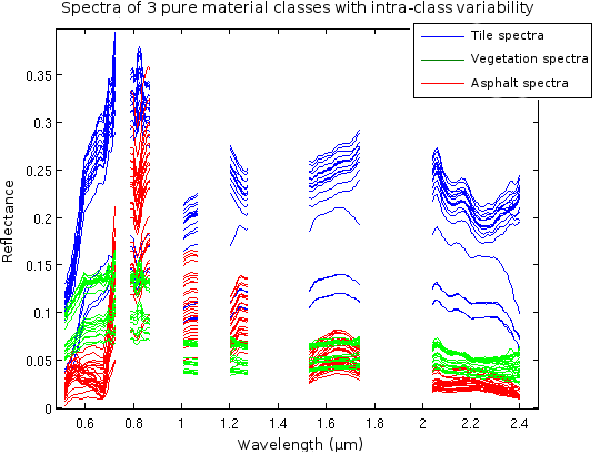
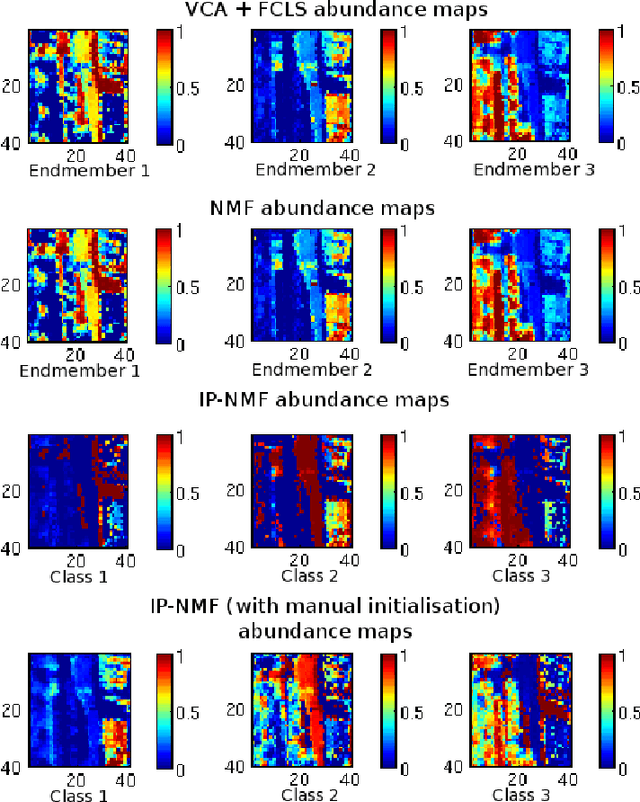
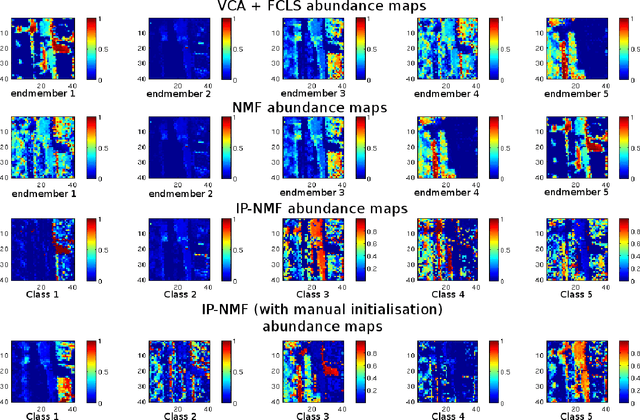
Blind source separation is a common processing tool to analyse the constitution of pixels of hyperspectral images. Such methods usually suppose that pure pixel spectra (endmembers) are the same in all the image for each class of materials. In the framework of remote sensing, such an assumption is no more valid in the presence of intra-class variabilities due to illumination conditions, weathering, slight variations of the pure materials, etc... In this paper, we first describe the results of investigations highlighting intra-class variability measured in real images. Considering these results, a new formulation of the linear mixing model is presented leading to two new methods. Unconstrained Pixel-by-pixel NMF (UP-NMF) is a new blind source separation method based on the assumption of a linear mixing model, which can deal with intra-class variability. To overcome UP-NMF limitations an extended method is proposed, named Inertia-constrained Pixel-by-pixel NMF (IP-NMF). For each sensed spectrum, these extended versions of NMF extract a corresponding set of source spectra. A constraint is set to limit the spreading of each source's estimates in IP-NMF. The methods are tested on a semi-synthetic data set built with spectra extracted from a real hyperspectral image and then numerically mixed. We thus demonstrate the interest of our methods for realistic source variabilities. Finally, IP-NMF is tested on a real data set and it is shown to yield better performance than state of the art methods.