Quantum process tomography with unknown single-preparation input states
Paper and Code
Sep 18, 2019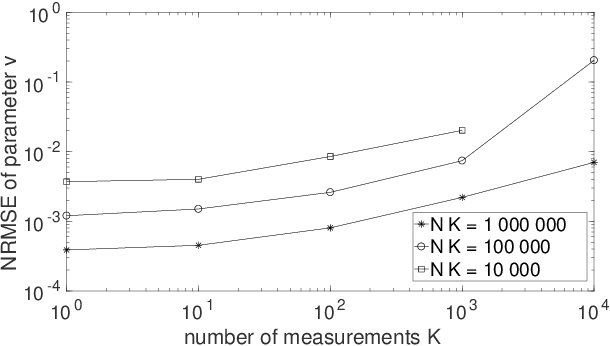
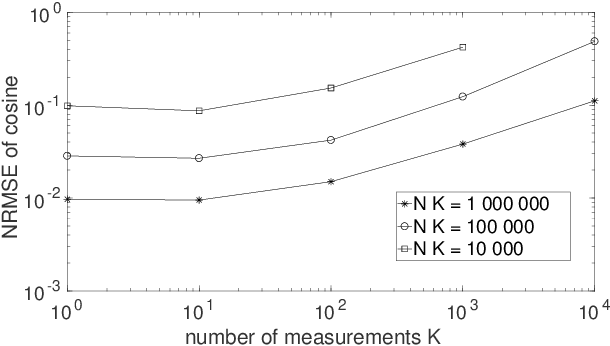
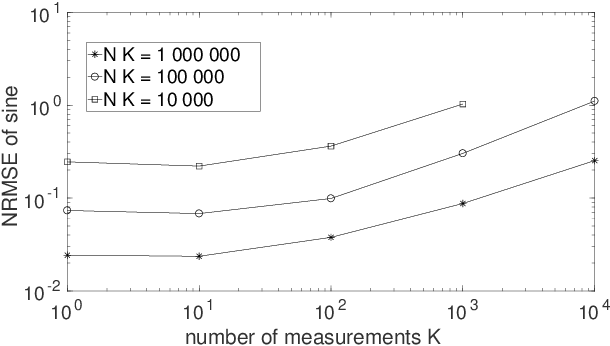
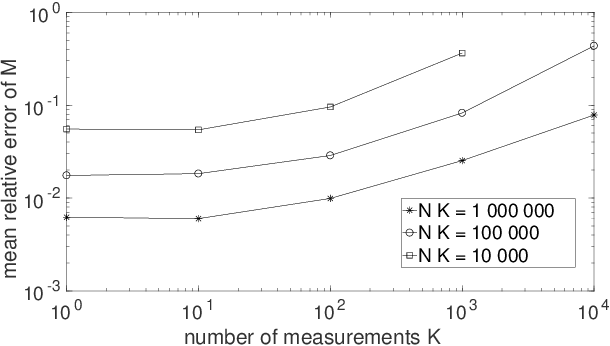
Quantum Process Tomography (QPT) methods aim at identifying, i.e. estimating, a given quantum process. QPT is a major quantum information processing tool, since it especially allows one to characterize the actual behavior of quantum gates, which are the building blocks of quantum computers. However, usual QPT procedures are complicated, since they set several constraints on the quantum states used as inputs of the process to be characterized. In this paper, we extend QPT so as to avoid two such constraints. On the one hand, usual QPT methods requires one to know, hence to precisely control (i.e. prepare), the specific quantum states used as inputs of the considered quantum process, which is cumbersome. We therefore propose a Blind, or unsupervised, extension of QPT (i.e. BQPT), which means that this approach uses input quantum states whose values are unknown and arbitrary, except that they are requested to meet some general known properties (and this approach exploits the output states of the considered quantum process). On the other hand, usual QPT methods require one to be able to prepare many copies of the same (known) input state, which is constraining. On the contrary, we propose "single-preparation methods", i.e. methods which can operate with only one instance of each considered input state. These two new concepts are here illustrated with practical BQPT methods which are numerically validated, in the case when: i) random pure states are used as inputs and their required properties are especially related to the statistical independence of the random variables that define them, ii) the considered quantum process is based on cylindrical-symmetry Heisenberg spin coupling. These concepts may be extended to a much wider class of processes and to BQPT methods based on other input quantum state properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge