Single-preparation unsupervised quantum machine learning: concepts and applications
Paper and Code
Jan 05, 2021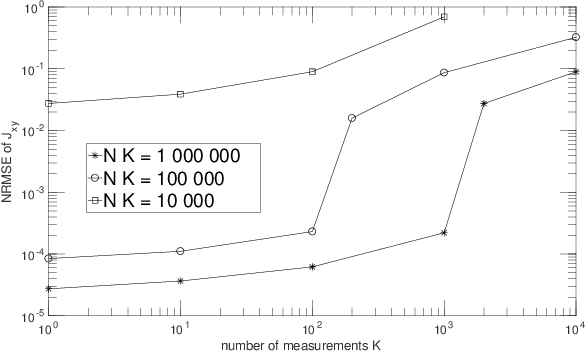
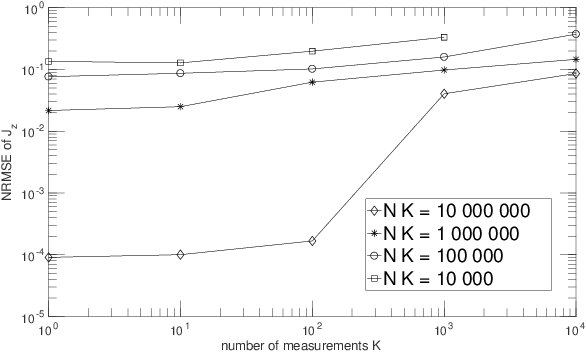
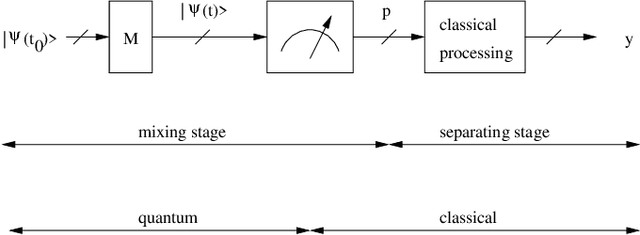
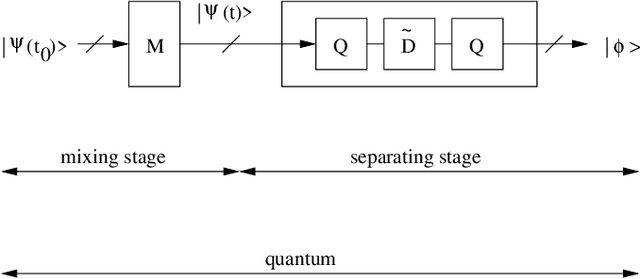
The term "machine learning" especially refers to algorithms that derive mappings, i.e. intput/output transforms, by using numerical data that provide information about considered transforms. These transforms appear in many problems, related to classification/clustering, regression, system identification, system inversion and input signal restoration/separation. We here first analyze the connections between all these problems, in the classical and quantum frameworks. We then focus on their most challenging versions, involving quantum data and/or quantum processing means, and unsupervised, i.e. blind, learning. Moreover, we propose the quite general concept of SIngle-Preparation Quantum Information Processing (SIPQIP). The resulting methods only require a single instance of each state, whereas usual methods have to very accurately create many copies of each fixed state. We apply our SIPQIP concept to various tasks, related to system identification (blind quantum process tomography or BQPT, blind Hamiltonian parameter estimation or BHPE, blind quantum channel identification/estimation, blind phase estimation), system inversion and state estimation (blind quantum source separation or BQSS, blind quantum entangled state restoration or BQSR, blind quantum channel equalization) and classification. Numerical tests show that our framework moreover yields much more accurate estimation than the standard multiple-preparation approach. Our methods are especially useful in a quantum computer, that we propose to more briefly call a "quamputer": BQPT and BHPE simplify the characterization of the gates of quamputers; BQSS and BQSR allow one to design quantum gates that may be used to compensate for the non-idealities that alter states stored in quantum registers, and they open the way to the much more general concept of self-adaptive quantum gates (see longer version of abstract in paper).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge