A Modified EXP3 and Its Adaptive Variant in Adversarial Bandits with Multi-User Delayed Feedback

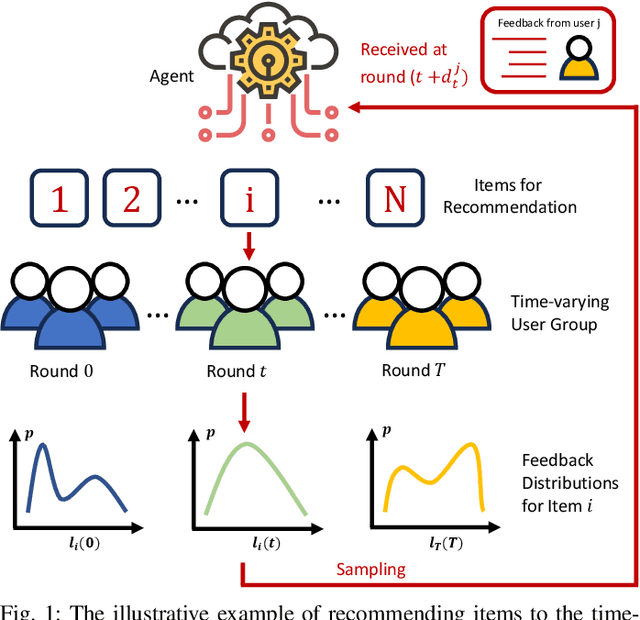
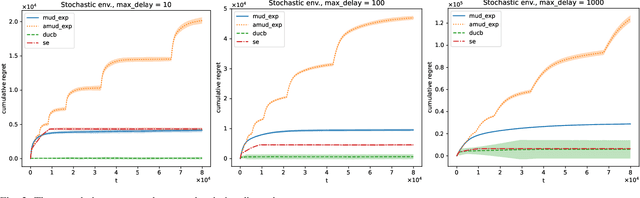
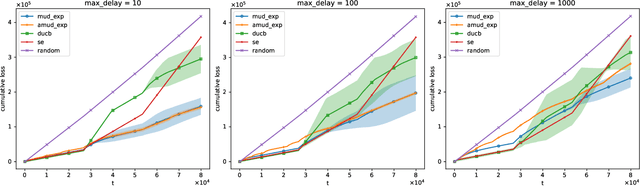
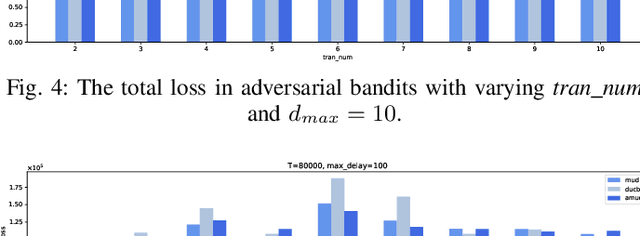
For the adversarial multi-armed bandit problem with delayed feedback, we consider that the delayed feedback results are from multiple users and are unrestricted on internal distribution. As the player picks an arm, feedback from multiple users may not be received instantly yet after an arbitrary delay of time which is unknown to the player in advance. For different users in a round, the delays in feedback have no latent correlation. Thus, we formulate an adversarial multi-armed bandit problem with multi-user delayed feedback and design a modified EXP3 algorithm named MUD-EXP3, which makes a decision at each round by considering the importance-weighted estimator of the received feedback from different users. On the premise of known terminal round index $T$, the number of users $M$, the number of arms $N$, and upper bound of delay $d_{max}$, we prove a regret of $\mathcal{O}(\sqrt{TM^2\ln{N}(N\mathrm{e}+4d_{max})})$. Furthermore, for the more common case of unknown $T$, an adaptive algorithm named AMUD-EXP3 is proposed with a sublinear regret with respect to $T$. Finally, extensive experiments are conducted to indicate the correctness and effectiveness of our algorithms.

A Survey on Influence Maximization: From an ML-Based Combinatorial Optimization

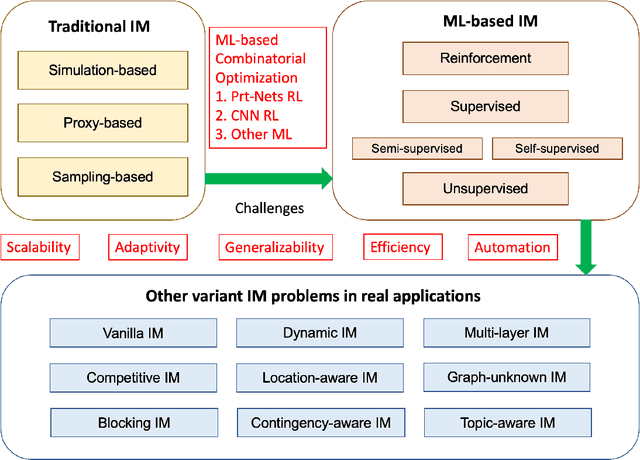
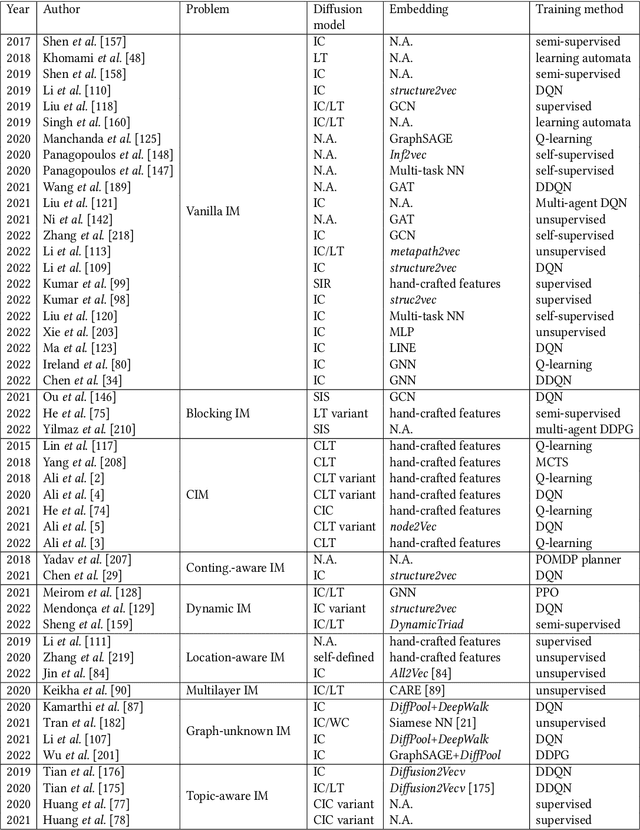
Influence Maximization (IM) is a classical combinatorial optimization problem, which can be widely used in mobile networks, social computing, and recommendation systems. It aims at selecting a small number of users such that maximizing the influence spread across the online social network. Because of its potential commercial and academic value, there are a lot of researchers focusing on studying the IM problem from different perspectives. The main challenge comes from the NP-hardness of the IM problem and \#P-hardness of estimating the influence spread, thus traditional algorithms for overcoming them can be categorized into two classes: heuristic algorithms and approximation algorithms. However, there is no theoretical guarantee for heuristic algorithms, and the theoretical design is close to the limit. Therefore, it is almost impossible to further optimize and improve their performance. With the rapid development of artificial intelligence, the technology based on Machine Learning (ML) has achieved remarkable achievements in many fields. In view of this, in recent years, a number of new methods have emerged to solve combinatorial optimization problems by using ML-based techniques. These methods have the advantages of fast solving speed and strong generalization ability to unknown graphs, which provide a brand-new direction for solving combinatorial optimization problems. Therefore, we abandon the traditional algorithms based on iterative search and review the recent development of ML-based methods, especially Deep Reinforcement Learning, to solve the IM problem and other variants in social networks. We focus on summarizing the relevant background knowledge, basic principles, common methods, and applied research. Finally, the challenges that need to be solved urgently in future IM research are pointed out.