A Modified EXP3 and Its Adaptive Variant in Adversarial Bandits with Multi-User Delayed Feedback
Paper and Code
Oct 17, 2023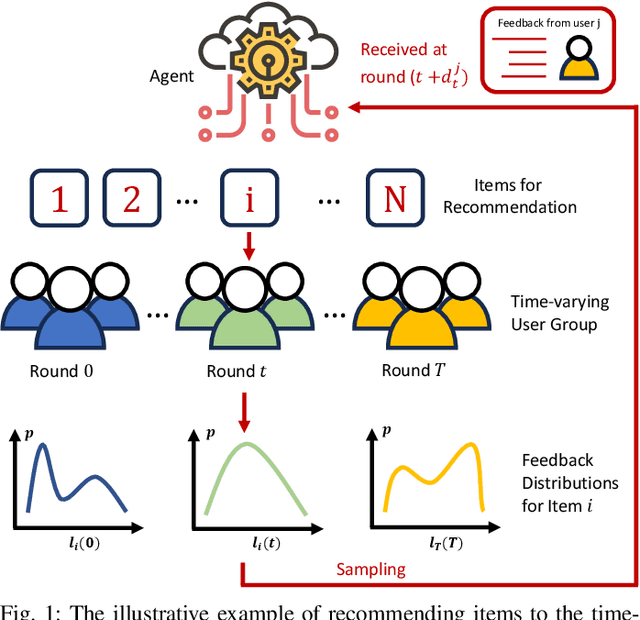
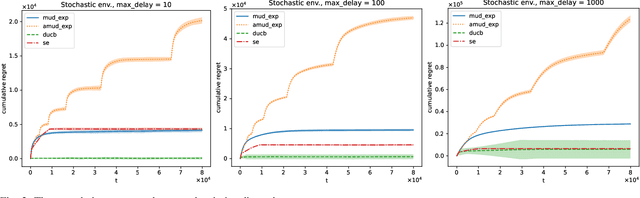
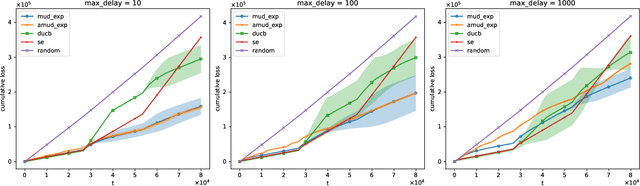
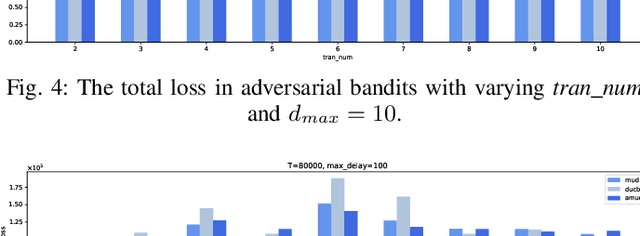
For the adversarial multi-armed bandit problem with delayed feedback, we consider that the delayed feedback results are from multiple users and are unrestricted on internal distribution. As the player picks an arm, feedback from multiple users may not be received instantly yet after an arbitrary delay of time which is unknown to the player in advance. For different users in a round, the delays in feedback have no latent correlation. Thus, we formulate an adversarial multi-armed bandit problem with multi-user delayed feedback and design a modified EXP3 algorithm named MUD-EXP3, which makes a decision at each round by considering the importance-weighted estimator of the received feedback from different users. On the premise of known terminal round index $T$, the number of users $M$, the number of arms $N$, and upper bound of delay $d_{max}$, we prove a regret of $\mathcal{O}(\sqrt{TM^2\ln{N}(N\mathrm{e}+4d_{max})})$. Furthermore, for the more common case of unknown $T$, an adaptive algorithm named AMUD-EXP3 is proposed with a sublinear regret with respect to $T$. Finally, extensive experiments are conducted to indicate the correctness and effectiveness of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge