Multi-Scale Subgraph Contrastive Learning

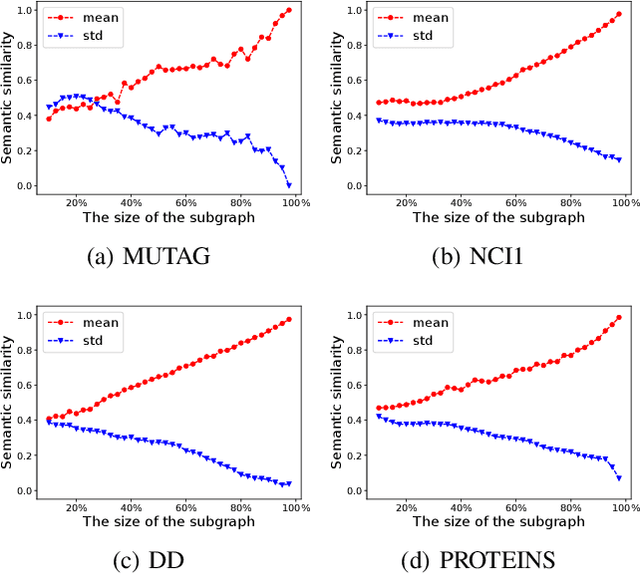
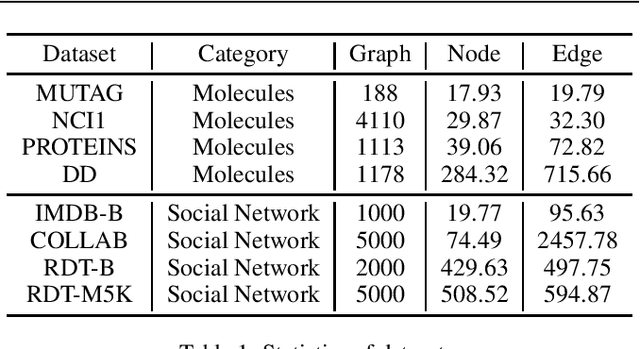
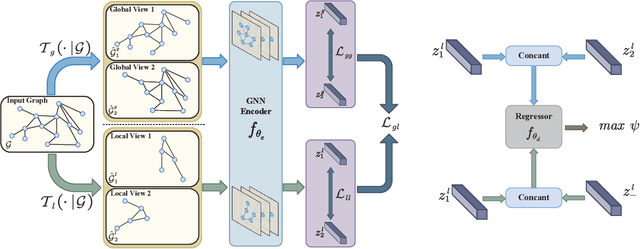
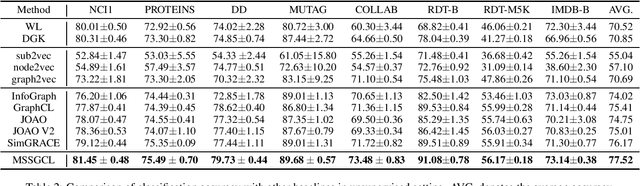
Graph-level contrastive learning, aiming to learn the representations for each graph by contrasting two augmented graphs, has attracted considerable attention. Previous studies usually simply assume that a graph and its augmented graph as a positive pair, otherwise as a negative pair. However, it is well known that graph structure is always complex and multi-scale, which gives rise to a fundamental question: after graph augmentation, will the previous assumption still hold in reality? By an experimental analysis, we discover the semantic information of an augmented graph structure may be not consistent as original graph structure, and whether two augmented graphs are positive or negative pairs is highly related with the multi-scale structures. Based on this finding, we propose a multi-scale subgraph contrastive learning method which is able to characterize the fine-grained semantic information. Specifically, we generate global and local views at different scales based on subgraph sampling, and construct multiple contrastive relationships according to their semantic associations to provide richer self-supervised signals. Extensive experiments and parametric analysis on eight graph classification real-world datasets well demonstrate the effectiveness of the proposed method.

Independence Promoted Graph Disentangled Networks

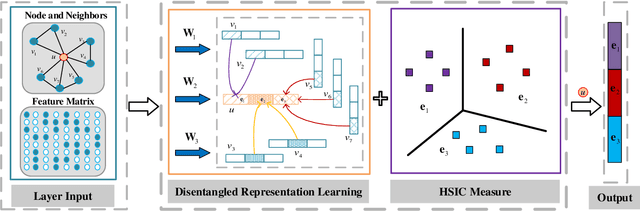
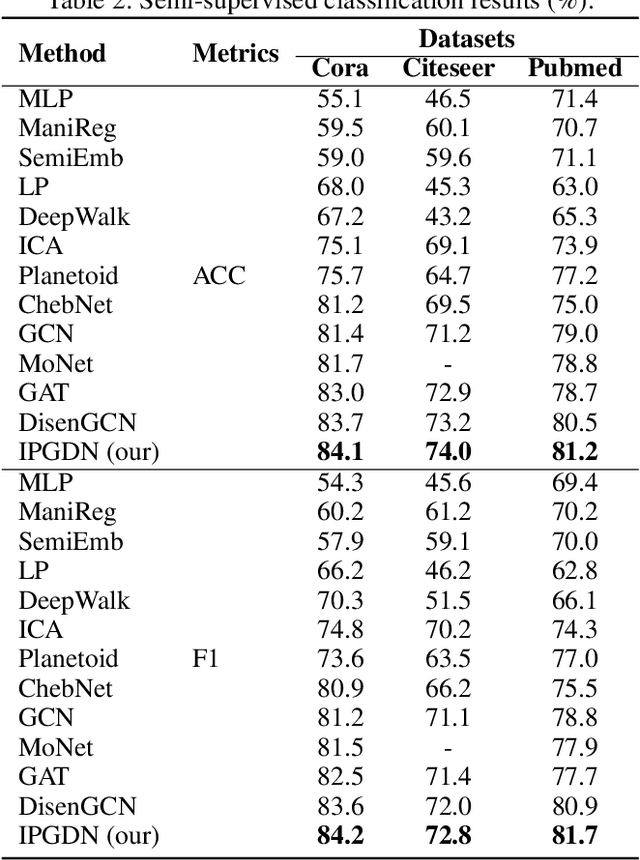
We address the problem of disentangled representation learning with independent latent factors in graph convolutional networks (GCNs). The current methods usually learn node representation by describing its neighborhood as a perceptual whole in a holistic manner while ignoring the entanglement of the latent factors. However, a real-world graph is formed by the complex interaction of many latent factors (e.g., the same hobby, education or work in social network). While little effort has been made toward exploring the disentangled representation in GCNs. In this paper, we propose a novel Independence Promoted Graph Disentangled Networks (IPGDN) to learn disentangled node representation while enhancing the independence among node representations. In particular, we firstly present disentangled representation learning by neighborhood routing mechanism, and then employ the Hilbert-Schmidt Independence Criterion (HSIC) to enforce independence between the latent representations, which is effectively integrated into a graph convolutional framework as a regularizer at the output layer. Experimental studies on real-world graphs validate our model and demonstrate that our algorithms outperform the state-of-the-arts by a wide margin in different network applications, including semi-supervised graph classification, graph clustering and graph visualization.