Independence Promoted Graph Disentangled Networks
Paper and Code
Nov 26, 2019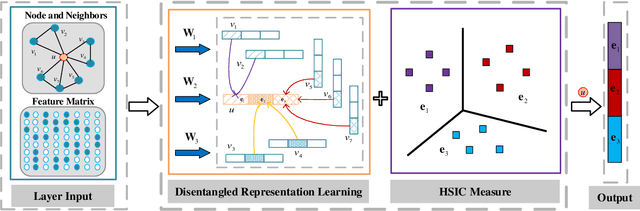
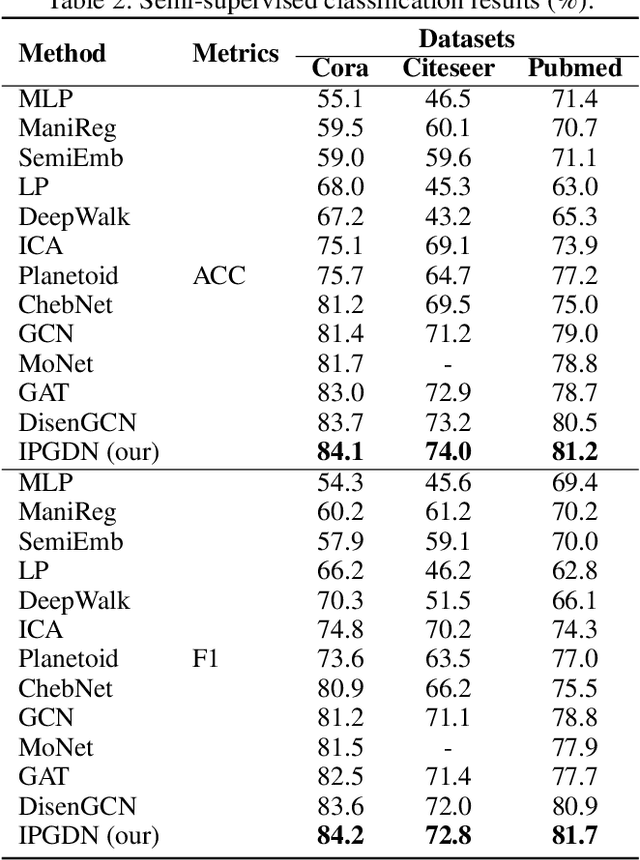

We address the problem of disentangled representation learning with independent latent factors in graph convolutional networks (GCNs). The current methods usually learn node representation by describing its neighborhood as a perceptual whole in a holistic manner while ignoring the entanglement of the latent factors. However, a real-world graph is formed by the complex interaction of many latent factors (e.g., the same hobby, education or work in social network). While little effort has been made toward exploring the disentangled representation in GCNs. In this paper, we propose a novel Independence Promoted Graph Disentangled Networks (IPGDN) to learn disentangled node representation while enhancing the independence among node representations. In particular, we firstly present disentangled representation learning by neighborhood routing mechanism, and then employ the Hilbert-Schmidt Independence Criterion (HSIC) to enforce independence between the latent representations, which is effectively integrated into a graph convolutional framework as a regularizer at the output layer. Experimental studies on real-world graphs validate our model and demonstrate that our algorithms outperform the state-of-the-arts by a wide margin in different network applications, including semi-supervised graph classification, graph clustering and graph visualization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge