Generalised Hyperbolic State-space Models for Inference in Dynamic Systems

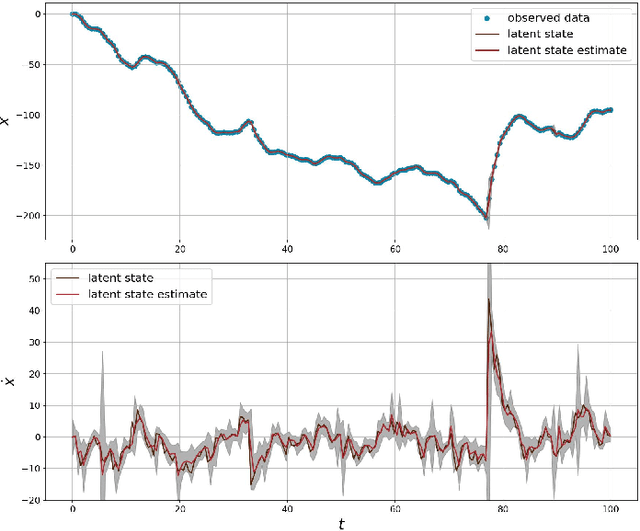
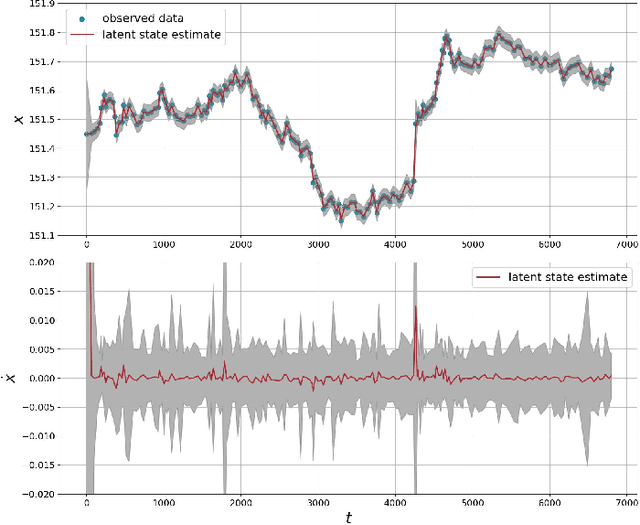
In this work we study linear vector stochastic differential equation (SDE) models driven by the generalised hyperbolic (GH) L\'evy process for inference in continuous-time non-Gaussian filtering problems. The GH family of stochastic processes offers a flexible framework for modelling of non-Gaussian, heavy-tailed characteristics and includes the normal inverse-Gaussian, variance-gamma and Student-t processes as special cases. We present continuous-time simulation methods for the solution of vector SDE models driven by GH processes and novel inference methodologies using a variant of sequential Markov chain Monte Carlo (MCMC). As an example a particular formulation of Langevin dynamics is studied within this framework. The model is applied to both a synthetically generated data set and a real-world financial series to demonstrate its capabilities.

Non-Gaussian Process Regression

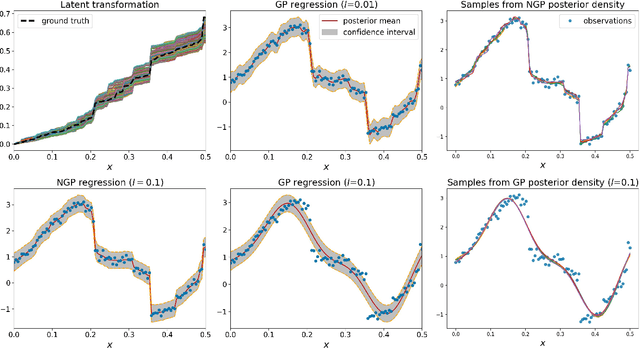
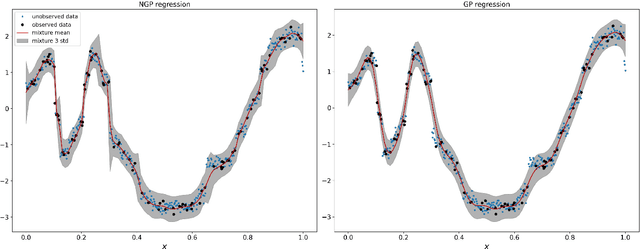
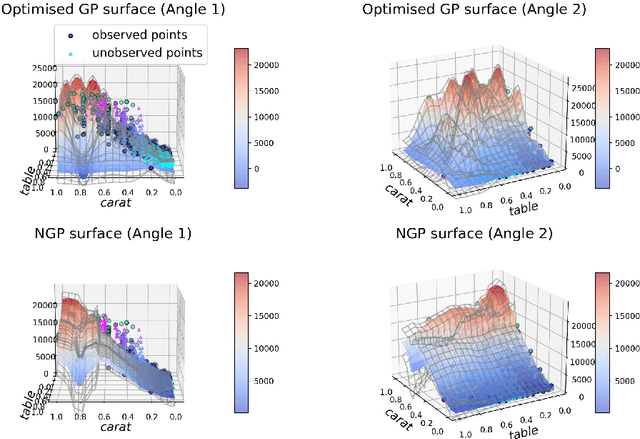
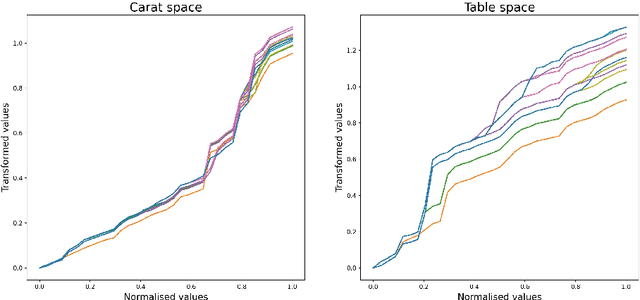
Standard GPs offer a flexible modelling tool for well-behaved processes. However, deviations from Gaussianity are expected to appear in real world datasets, with structural outliers and shocks routinely observed. In these cases GPs can fail to model uncertainty adequately and may over-smooth inferences. Here we extend the GP framework into a new class of time-changed GPs that allow for straightforward modelling of heavy-tailed non-Gaussian behaviours, while retaining a tractable conditional GP structure through an infinite mixture of non-homogeneous GPs representation. The conditional GP structure is obtained by conditioning the observations on a latent transformed input space and the random evolution of the latent transformation is modelled using a L\'{e}vy process which allows Bayesian inference in both the posterior predictive density and the latent transformation function. We present Markov chain Monte Carlo inference procedures for this model and demonstrate the potential benefits compared to a standard GP.

Point process simulation of Generalised inverse Gaussian processes and estimation of the Jaeger Integral

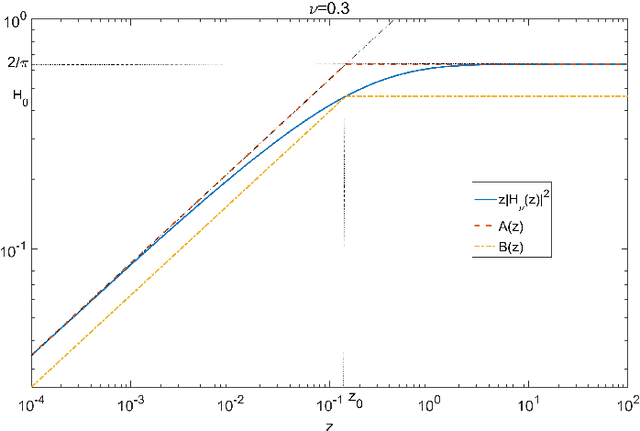
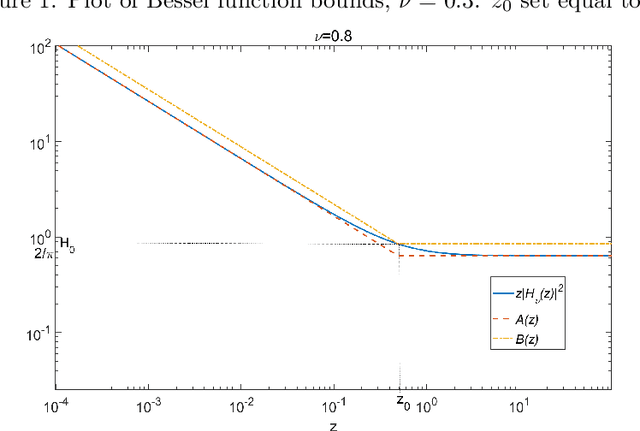
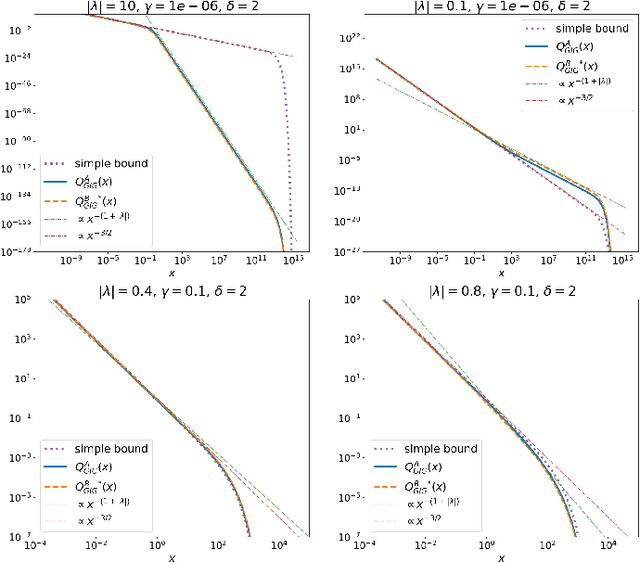
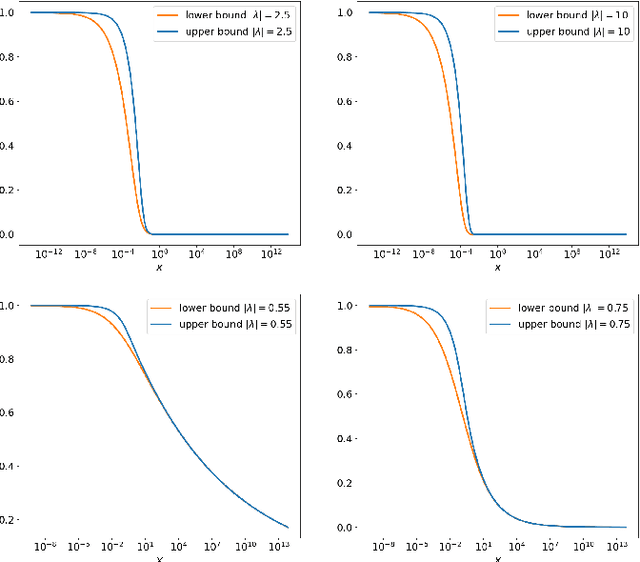
In this paper novel simulation methods are provided for the Generalised inverse Gaussian (GIG) L\'{e}vy process. Such processes are intractable for simulation except in certain special edge cases, since the L\'{e}vy density associated with the GIG process is expressed as an integral involving certain Bessel Functions, known as the Jaeger Integral in diffusive transport applications. We here show for the first time how to solve the problem indirectly, using generalised shot-noise methods to simulate the underlying point processes and constructing an auxiliary variables approach that avoids any direct calculation of the integrals involved. The augmented bivariate process is still intractable and so we propose a novel thinning method based on upper bounds on the intractable integrand. Moreover our approach leads to lower and upper bounds on the Jaeger integral itself, which may be compared with other approximation methods. We note that the GIG process is the required Brownian motion subordinator for the generalised hyperbolic (GH) L\'{e}vy process and so our simulation approach will straightforwardly extend also to the simulation of these intractable proceses. Our new methods will find application in forward simulation of processes of GIG and GH type, in financial and engineering data, for example, as well as inference for states and parameters of stochastic processes driven by GIG and GH L\'{e}vy processes.