Generalised Hyperbolic State-space Models for Inference in Dynamic Systems

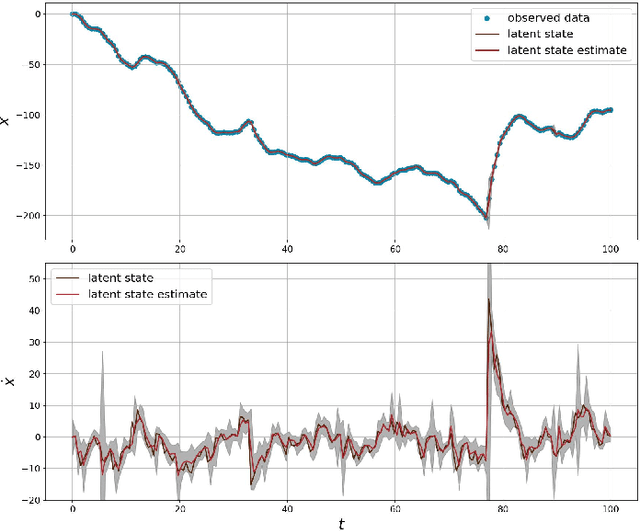
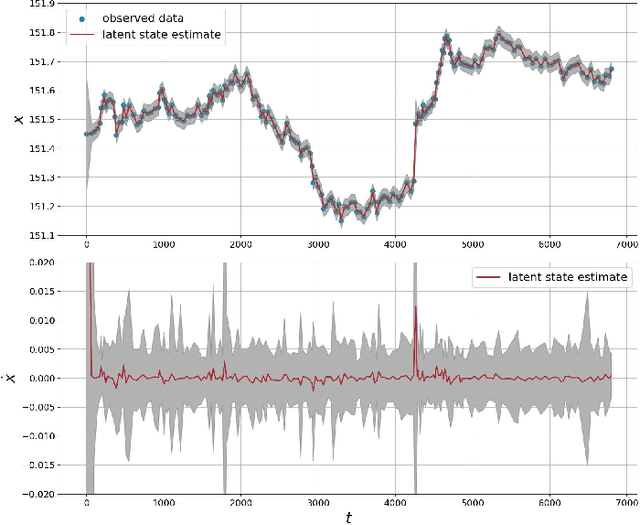
In this work we study linear vector stochastic differential equation (SDE) models driven by the generalised hyperbolic (GH) L\'evy process for inference in continuous-time non-Gaussian filtering problems. The GH family of stochastic processes offers a flexible framework for modelling of non-Gaussian, heavy-tailed characteristics and includes the normal inverse-Gaussian, variance-gamma and Student-t processes as special cases. We present continuous-time simulation methods for the solution of vector SDE models driven by GH processes and novel inference methodologies using a variant of sequential Markov chain Monte Carlo (MCMC). As an example a particular formulation of Langevin dynamics is studied within this framework. The model is applied to both a synthetically generated data set and a real-world financial series to demonstrate its capabilities.