Non-Gaussian Process Regression
Paper and Code
Sep 07, 2022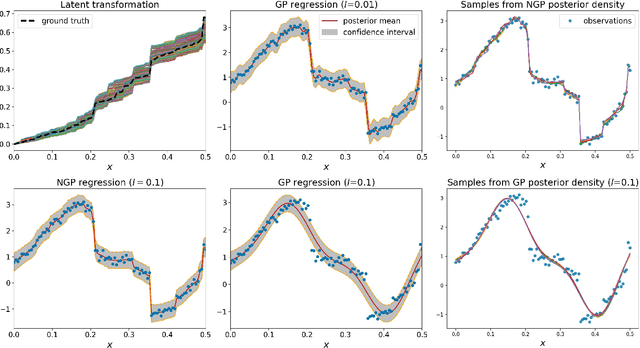
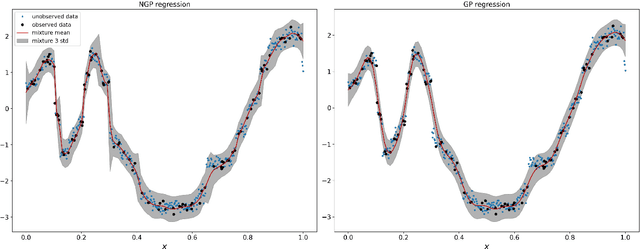
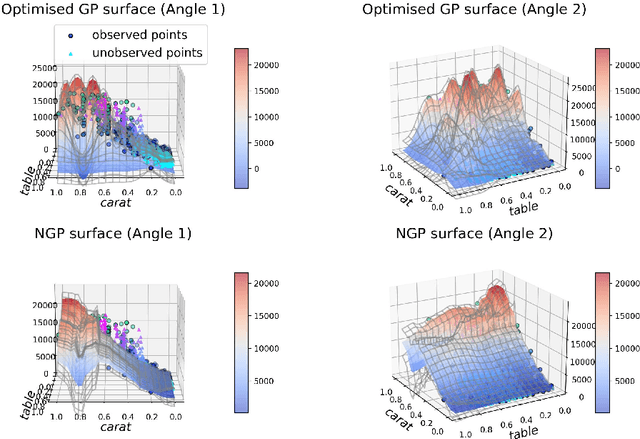
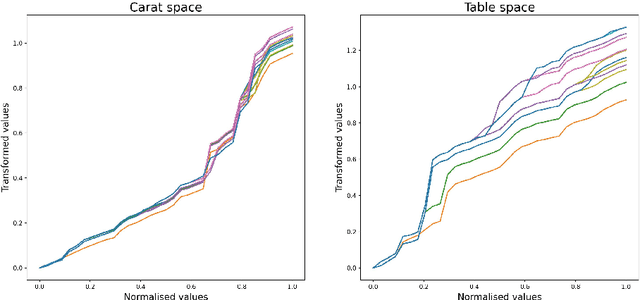
Standard GPs offer a flexible modelling tool for well-behaved processes. However, deviations from Gaussianity are expected to appear in real world datasets, with structural outliers and shocks routinely observed. In these cases GPs can fail to model uncertainty adequately and may over-smooth inferences. Here we extend the GP framework into a new class of time-changed GPs that allow for straightforward modelling of heavy-tailed non-Gaussian behaviours, while retaining a tractable conditional GP structure through an infinite mixture of non-homogeneous GPs representation. The conditional GP structure is obtained by conditioning the observations on a latent transformed input space and the random evolution of the latent transformation is modelled using a L\'{e}vy process which allows Bayesian inference in both the posterior predictive density and the latent transformation function. We present Markov chain Monte Carlo inference procedures for this model and demonstrate the potential benefits compared to a standard GP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge