Xupeng Shi
Finding Dynamics Preserving Adversarial Winning Tickets
Mar 06, 2022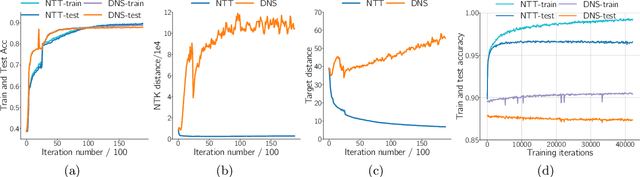
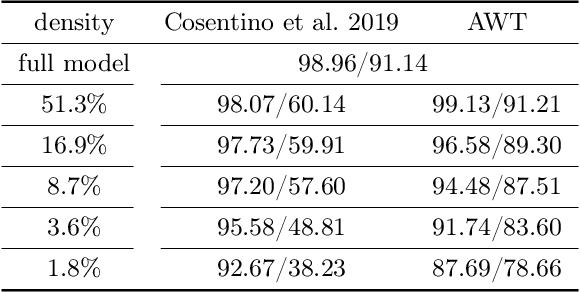
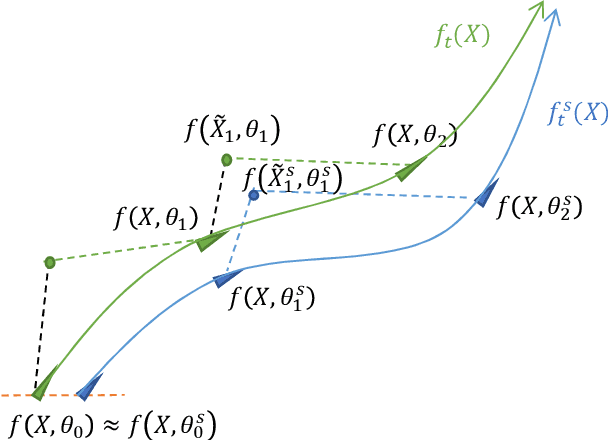
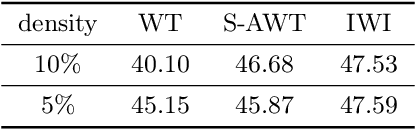
Abstract:Modern deep neural networks (DNNs) are vulnerable to adversarial attacks and adversarial training has been shown to be a promising method for improving the adversarial robustness of DNNs. Pruning methods have been considered in adversarial context to reduce model capacity and improve adversarial robustness simultaneously in training. Existing adversarial pruning methods generally mimic the classical pruning methods for natural training, which follow the three-stage 'training-pruning-fine-tuning' pipelines. We observe that such pruning methods do not necessarily preserve the dynamics of dense networks, making it potentially hard to be fine-tuned to compensate the accuracy degradation in pruning. Based on recent works of \textit{Neural Tangent Kernel} (NTK), we systematically study the dynamics of adversarial training and prove the existence of trainable sparse sub-network at initialization which can be trained to be adversarial robust from scratch. This theoretically verifies the \textit{lottery ticket hypothesis} in adversarial context and we refer such sub-network structure as \textit{Adversarial Winning Ticket} (AWT). We also show empirical evidences that AWT preserves the dynamics of adversarial training and achieve equal performance as dense adversarial training.
Understanding and Quantifying Adversarial Examples Existence in Linear Classification
Oct 27, 2019



Abstract:State-of-art deep neural networks (DNN) are vulnerable to attacks by adversarial examples: a carefully designed small perturbation to the input, that is imperceptible to human, can mislead DNN. To understand the root cause of adversarial examples, we quantify the probability of adversarial example existence for linear classifiers. Previous mathematical definition of adversarial examples only involves the overall perturbation amount, and we propose a more practical relevant definition of strong adversarial examples that separately limits the perturbation along the signal direction also. We show that linear classifiers can be made robust to strong adversarial examples attack in cases where no adversarial robust linear classifiers exist under the previous definition. The quantitative formulas are confirmed by numerical experiments using a linear support vector machine (SVM) classifier. The results suggest that designing general strong-adversarial-robust learning systems is feasible but only through incorporating human knowledge of the underlying classification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge