Task-Adaptive Parameter-Efficient Fine-Tuning for Weather Foundation Models

While recent advances in machine learning have equipped Weather Foundation Models (WFMs) with substantial generalization capabilities across diverse downstream tasks, the escalating computational requirements associated with their expanding scale increasingly hinder practical deployment. Current Parameter-Efficient Fine-Tuning (PEFT) methods, designed for vision or language tasks, fail to address the unique challenges of weather downstream tasks, such as variable heterogeneity, resolution diversity, and spatiotemporal coverage variations, leading to suboptimal performance when applied to WFMs. To bridge this gap, we introduce WeatherPEFT, a novel PEFT framework for WFMs incorporating two synergistic innovations. First, during the forward pass, Task-Adaptive Dynamic Prompting (TADP) dynamically injects the embedding weights within the encoder to the input tokens of the pre-trained backbone via internal and external pattern extraction, enabling context-aware feature recalibration for specific downstream tasks. Furthermore, during backpropagation, Stochastic Fisher-Guided Adaptive Selection (SFAS) not only leverages Fisher information to identify and update the most task-critical parameters, thereby preserving invariant pre-trained knowledge, but also introduces randomness to stabilize the selection. We demonstrate the effectiveness and efficiency of WeatherPEFT on three downstream tasks, where existing PEFT methods show significant gaps versus Full-Tuning, and WeatherPEFT achieves performance parity with Full-Tuning using fewer trainable parameters. The code of this work will be released.

Degree of Staleness-Aware Data Updating in Federated Learning

Handling data staleness remains a significant challenge in federated learning with highly time-sensitive tasks, where data is generated continuously and data staleness largely affects model performance. Although recent works attempt to optimize data staleness by determining local data update frequency or client selection strategy, none of them explore taking both data staleness and data volume into consideration. In this paper, we propose DUFL(Data Updating in Federated Learning), an incentive mechanism featuring an innovative local data update scheme manipulated by three knobs: the server's payment, outdated data conservation rate, and clients' fresh data collection volume, to coordinate staleness and volume of local data for best utilities. To this end, we introduce a novel metric called DoS(the Degree of Staleness) to quantify data staleness and conduct a theoretic analysis illustrating the quantitative relationship between DoS and model performance. We model DUFL as a two-stage Stackelberg game with dynamic constraint, deriving the optimal local data update strategy for each client in closed-form and the approximately optimal strategy for the server. Experimental results on real-world datasets demonstrate the significant performance of our approach.

Multi-Hop Privacy Propagation for Differentially Private Federated Learning in Social Networks

Federated learning (FL) enables collaborative model training across decentralized clients without sharing local data, thereby enhancing privacy and facilitating collaboration among clients connected via social networks. However, these social connections introduce privacy externalities: a client's privacy loss depends not only on its privacy protection strategy but also on the privacy decisions of others, propagated through the network via multi-hop interactions. In this work, we propose a socially-aware privacy-preserving FL mechanism that systematically quantifies indirect privacy leakage through a multi-hop propagation model. We formulate the server-client interaction as a two-stage Stackelberg game, where the server, as the leader, optimizes incentive policies, and clients, as followers, strategically select their privacy budgets, which determine their privacy-preserving levels by controlling the magnitude of added noise. To mitigate information asymmetry in networked privacy estimation, we introduce a mean-field estimator to approximate the average external privacy risk. We theoretically prove the existence and convergence of the fixed point of the mean-field estimator and derive closed-form expressions for the Stackelberg Nash Equilibrium. Despite being designed from a client-centric incentive perspective, our mechanism achieves approximately-optimal social welfare, as revealed by Price of Anarchy (PoA) analysis. Experiments on diverse datasets demonstrate that our approach significantly improves client utilities and reduces server costs while maintaining model performance, outperforming both Social-Agnostic (SA) baselines and methods that account for social externalities.

Adaptive Federated Learning via New Entropy Approach

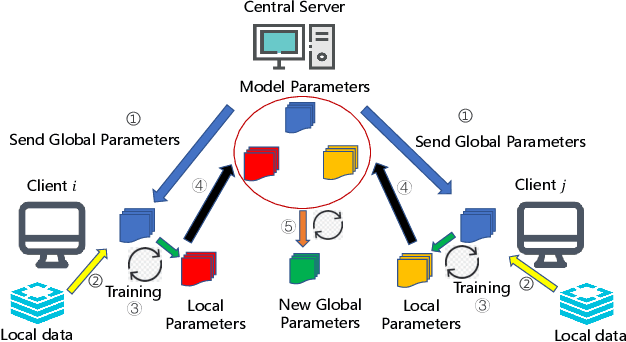
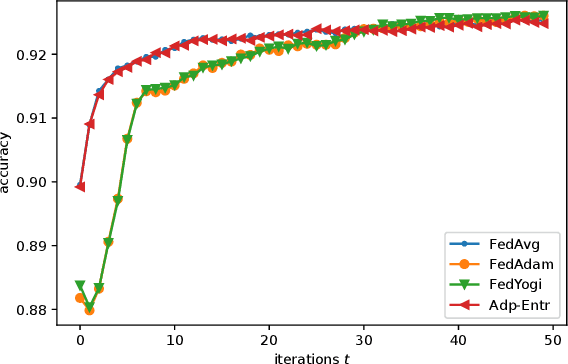
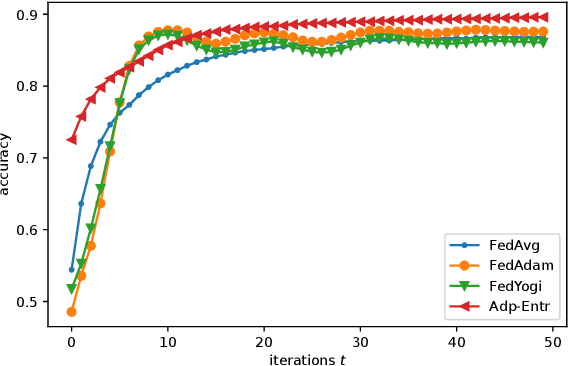
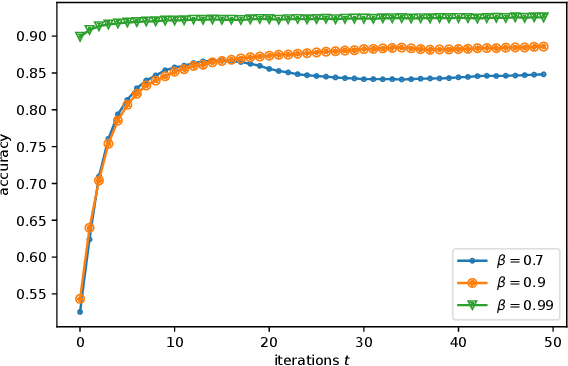
Federated Learning (FL) has recently emerged as a popular framework, which allows resource-constrained discrete clients to cooperatively learn the global model under the orchestration of a central server while storing privacy-sensitive data locally. However, due to the difference in equipment and data divergence of heterogeneous clients, there will be parameter deviation between local models, resulting in a slow convergence rate and a reduction of the accuracy of the global model. The current FL algorithms use the static client learning strategy pervasively and can not adapt to the dynamic training parameters of different clients. In this paper, by considering the deviation between different local model parameters, we propose an adaptive learning rate scheme for each client based on entropy theory to alleviate the deviation between heterogeneous clients and achieve fast convergence of the global model. It's difficult to design the optimal dynamic learning rate for each client as the local information of other clients is unknown, especially during the local training epochs without communications between local clients and the central server. To enable a decentralized learning rate design for each client, we first introduce mean-field schemes to estimate the terms related to other clients' local model parameters. Then the decentralized adaptive learning rate for each client is obtained in closed form by constructing the Hamilton equation. Moreover, we prove that there exist fixed point solutions for the mean-field estimators, and an algorithm is proposed to obtain them. Finally, extensive experimental results on real datasets show that our algorithm can effectively eliminate the deviation between local model parameters compared to other recent FL algorithms.

Fast Convergent Federated Learning with Aggregated Gradients

Federated Learning (FL) is a novel machine learning framework, which enables multiple distributed devices cooperatively to train a shared model scheduled by a central server while protecting private data locally. However, the non-independent-and-identically-distributed (Non-IID) data samples and frequent communication across participants may significantly slow down the convergent rate and increase communication costs. To achieve fast convergence, we ameliorate the conventional local updating rule by introducing the aggregated gradients at each local update epoch, and propose an adaptive learning rate algorithm that further takes the deviation of local parameter and global parameter into consideration. The above adaptive learning rate design requires all clients' local information including the local parameters and gradients, which is challenging as there is no communication during the local update epochs. To obtain a decentralized adaptive learning rate for each client, we utilize the mean field approach by introducing two mean field terms to estimate the average local parameters and gradients respectively, which does not require the clients to exchange their local information with each other at each local epoch. Numerical results show that our proposed framework is superior to the state-of-art FL schemes in both model accuracy and convergent rate for IID and Non-IID datasets.