Adaptive Federated Learning via New Entropy Approach

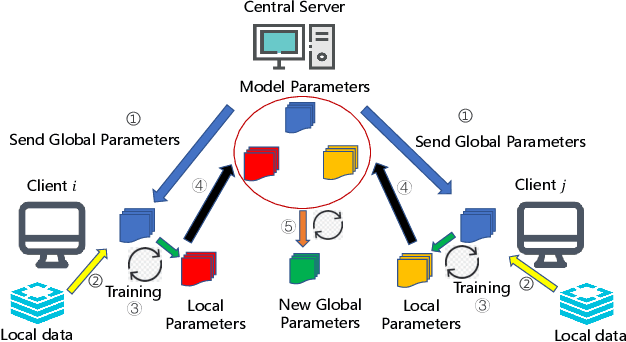
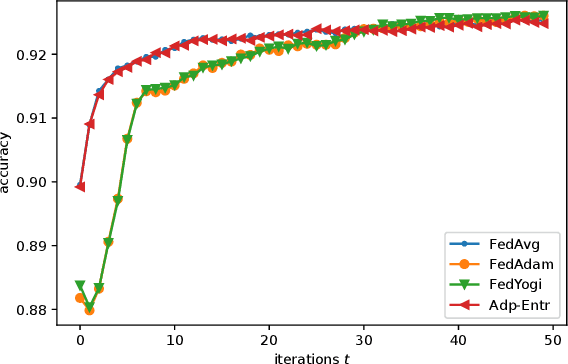
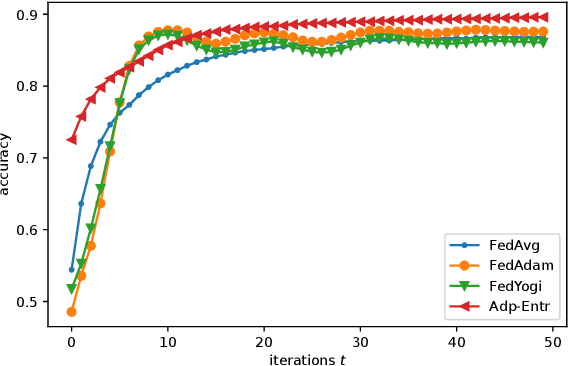
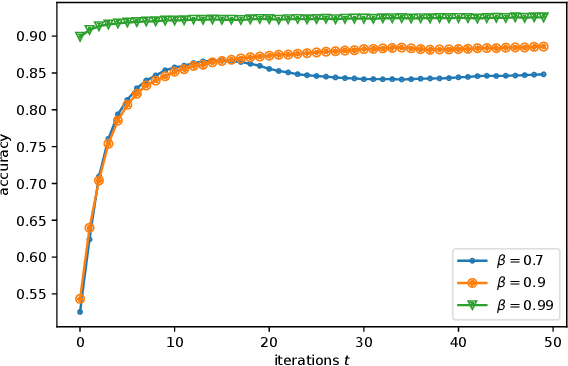
Federated Learning (FL) has recently emerged as a popular framework, which allows resource-constrained discrete clients to cooperatively learn the global model under the orchestration of a central server while storing privacy-sensitive data locally. However, due to the difference in equipment and data divergence of heterogeneous clients, there will be parameter deviation between local models, resulting in a slow convergence rate and a reduction of the accuracy of the global model. The current FL algorithms use the static client learning strategy pervasively and can not adapt to the dynamic training parameters of different clients. In this paper, by considering the deviation between different local model parameters, we propose an adaptive learning rate scheme for each client based on entropy theory to alleviate the deviation between heterogeneous clients and achieve fast convergence of the global model. It's difficult to design the optimal dynamic learning rate for each client as the local information of other clients is unknown, especially during the local training epochs without communications between local clients and the central server. To enable a decentralized learning rate design for each client, we first introduce mean-field schemes to estimate the terms related to other clients' local model parameters. Then the decentralized adaptive learning rate for each client is obtained in closed form by constructing the Hamilton equation. Moreover, we prove that there exist fixed point solutions for the mean-field estimators, and an algorithm is proposed to obtain them. Finally, extensive experimental results on real datasets show that our algorithm can effectively eliminate the deviation between local model parameters compared to other recent FL algorithms.