Bayesian Multistate Bennett Acceptance Ratio Methods

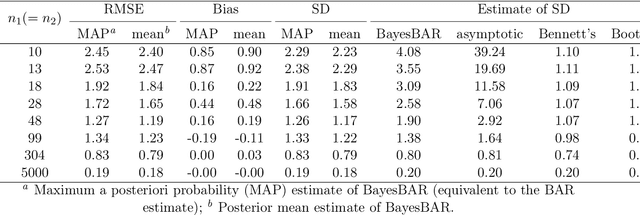
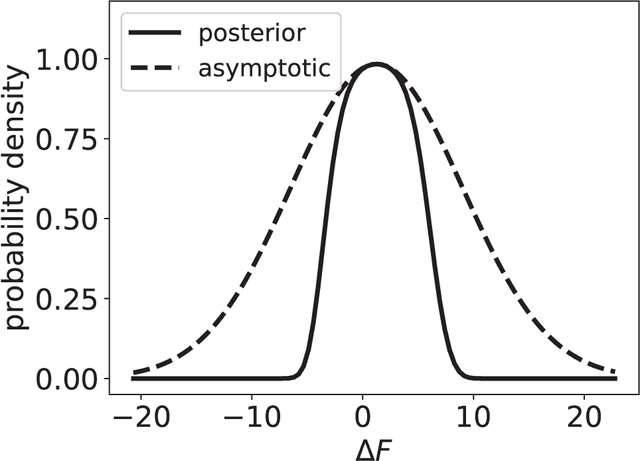
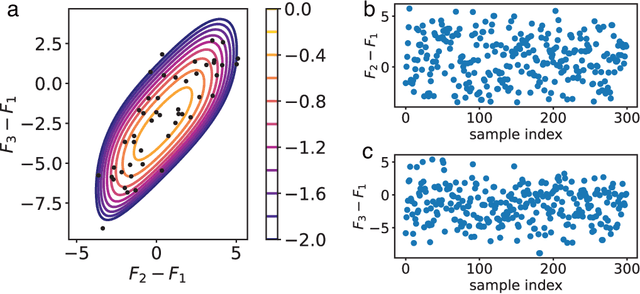
The multistate Bennett acceptance ratio (MBAR) method is a prevalent approach for computing free energies of thermodynamic states. In this work, we introduce BayesMBAR, a Bayesian generalization of the MBAR method. By integrating configurations sampled from thermodynamic states with a prior distribution, BayesMBAR computes a posterior distribution of free energies. Using the posterior distribution, we derive free energy estimations and compute their associated uncertainties. Notably, when a uniform prior distribution is used, BayesMBAR recovers the MBAR's result but provides more accurate uncertainty estimates. Additionally, when prior knowledge about free energies is available, BayesMBAR can incorporate this information into the estimation procedure by using non-uniform prior distributions. As an example, we show that, by incorporating the prior knowledge about the smoothness of free energy surfaces, BayesMBAR provides more accurate estimates than the MBAR method. Given MBAR's widespread use in free energy calculations, we anticipate BayesMBAR to be an essential tool in various applications of free energy calculations.

Contrastive Learning of Coarse-Grained Force Fields

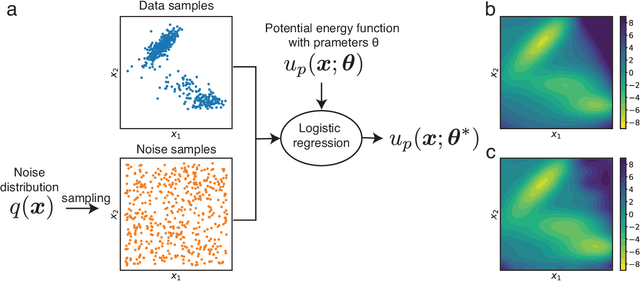
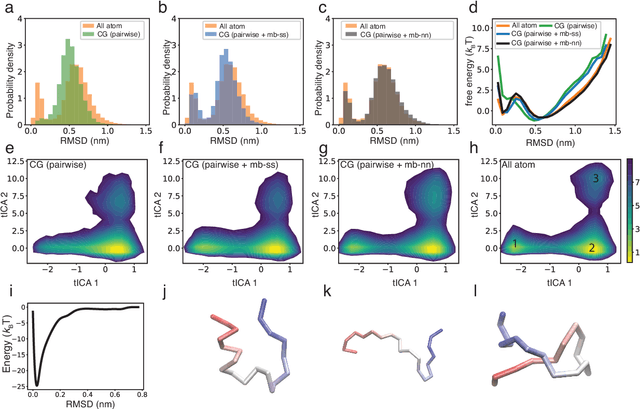
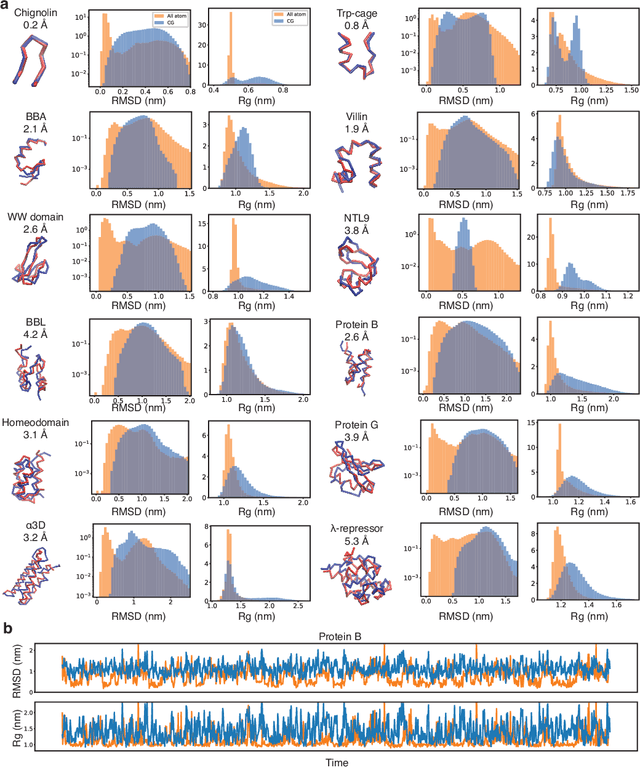
Coarse-grained models have proven helpful for simulating complex systems over long timescales to provide molecular insights into various processes. Methodologies for systematic parameterization of the underlying energy function, or force field that describes the interactions among different components of the system are of great interest for ensuring simulation accuracy. We present a new method, potential contrasting, to enable efficient learning of force fields that can accurately reproduce the conformational distribution produced with all-atom simulations. Potential contrasting generalizes the noise contrastive estimation method with umbrella sampling to better learn the complex energy landscape of molecular systems. When applied to the Trp-cage protein, we found that the technique produces force fields that thoroughly capture the thermodynamics of the folding process despite the use of only $\alpha$-Carbons in the coarse-grained model. We further showed that potential contrasting could be applied over large datasets that combine the conformational ensembles of many proteins to ensure the transferability of coarse-grained force fields. We anticipate potential contrasting to be a powerful tool for building general-purpose coarse-grained force fields.

Computing Absolute Free Energy with Deep Generative Models

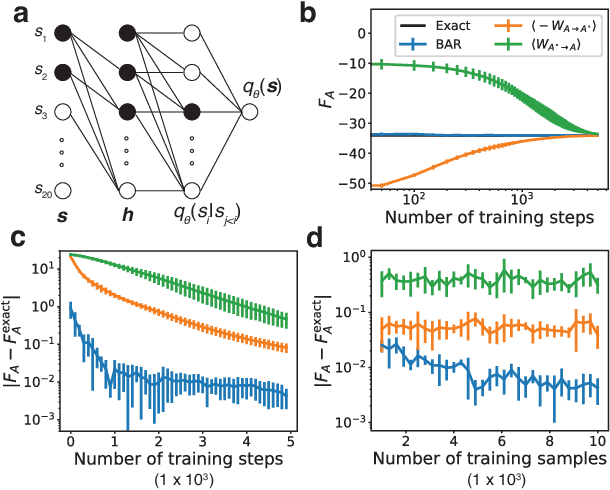
Fast and accurate evaluation of free energy has broad applications from drug design to material engineering. Computing the absolute free energy is of particular interest since it allows the assessment of the relative stability between states without the use of intermediates. In this letter, we introduce a general framework for calculating the absolute free energy of a state. A key step of the calculation is the definition of a reference state with tractable deep generative models using locally sampled configurations. The absolute free energy of this reference state is zero by design. The free energy for the state of interest can then be determined as the difference from the reference. We applied this approach to both discrete and continuous systems and demonstrated its effectiveness. It was found that the Bennett acceptance ratio method provides more accurate and efficient free energy estimations than approximate expressions based on work. We anticipate the method presented here to be a valuable strategy for computing free energy differences.

Improving Importance Weighted Auto-Encoders with Annealed Importance Sampling

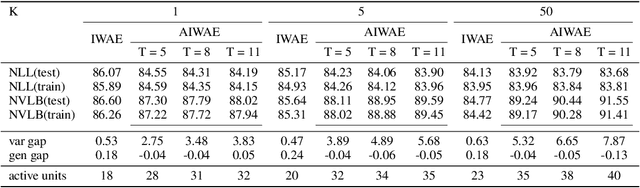
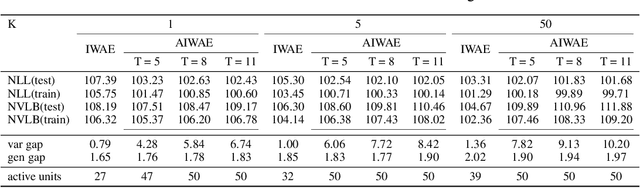
Stochastic variational inference with an amortized inference model and the reparameterization trick has become a widely-used algorithm for learning latent variable models. Increasing the flexibility of approximate posterior distributions while maintaining computational tractability is one of the core problems in stochastic variational inference. Two families of approaches proposed to address the problem are flow-based and multisample-based approaches such as importance weighted auto-encoders (IWAE). We introduce a new learning algorithm, the annealed importance weighted auto-encoder (AIWAE), for learning latent variable models. The proposed AIWAE combines multisample-based and flow-based approaches with the annealed importance sampling and its memory cost stays constant when the depth of flows increases. The flow constructed using an annealing process in AIWAE facilitates the exploration of the latent space when the posterior distribution has multiple modes. Through computational experiments, we show that, compared to models trained using the IWAE, AIWAE-trained models are better density models, have more complex posterior distributions and use more latent space representation capacity.