Improving Importance Weighted Auto-Encoders with Annealed Importance Sampling

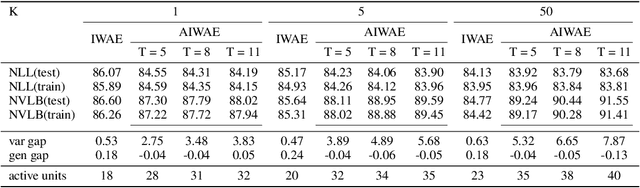
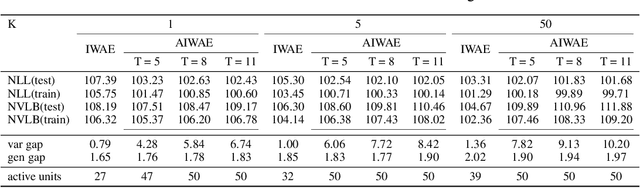
Stochastic variational inference with an amortized inference model and the reparameterization trick has become a widely-used algorithm for learning latent variable models. Increasing the flexibility of approximate posterior distributions while maintaining computational tractability is one of the core problems in stochastic variational inference. Two families of approaches proposed to address the problem are flow-based and multisample-based approaches such as importance weighted auto-encoders (IWAE). We introduce a new learning algorithm, the annealed importance weighted auto-encoder (AIWAE), for learning latent variable models. The proposed AIWAE combines multisample-based and flow-based approaches with the annealed importance sampling and its memory cost stays constant when the depth of flows increases. The flow constructed using an annealing process in AIWAE facilitates the exploration of the latent space when the posterior distribution has multiple modes. Through computational experiments, we show that, compared to models trained using the IWAE, AIWAE-trained models are better density models, have more complex posterior distributions and use more latent space representation capacity.