AI-Empowered Human Research Integrating Brain Science and Social Sciences Insights

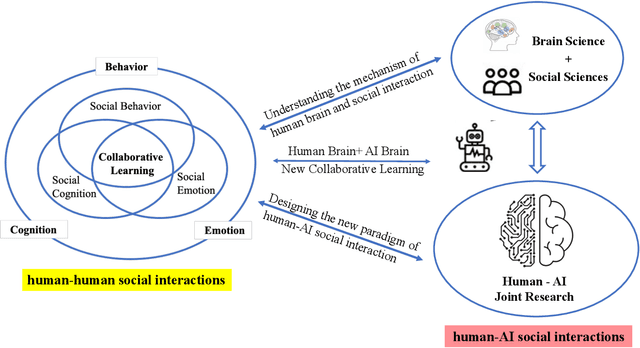
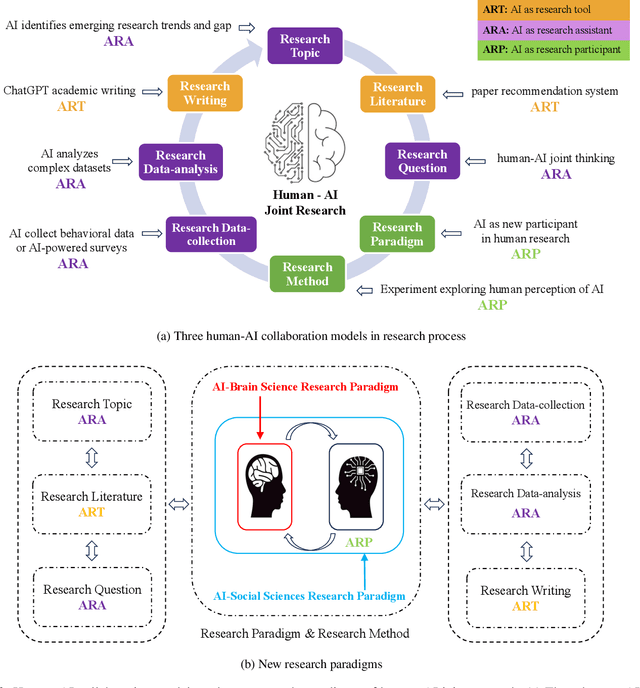
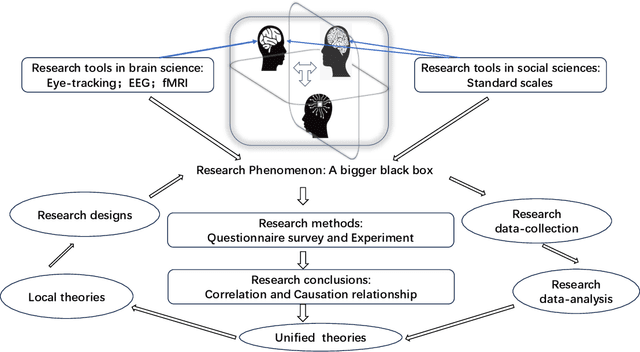
This paper explores the transformative role of artificial intelligence (AI) in enhancing scientific research, particularly in the fields of brain science and social sciences. We analyze the fundamental aspects of human research and argue that it is high time for researchers to transition to human-AI joint research. Building upon this foundation, we propose two innovative research paradigms of human-AI joint research: "AI-Brain Science Research Paradigm" and "AI-Social Sciences Research Paradigm". In these paradigms, we introduce three human-AI collaboration models: AI as a research tool (ART), AI as a research assistant (ARA), and AI as a research participant (ARP). Furthermore, we outline the methods for conducting human-AI joint research. This paper seeks to redefine the collaborative interactions between human researchers and AI system, setting the stage for future research directions and sparking innovation in this interdisciplinary field.

A Theoretical Review on Solving Algebra Problems

Solving algebra problems (APs) continues to attract significant research interest as evidenced by the large number of algorithms and theories proposed over the past decade. Despite these important research contributions, however, the body of work remains incomplete in terms of theoretical justification and scope. The current contribution intends to fill the gap by developing a review framework that aims to lay a theoretical base, create an evaluation scheme, and extend the scope of the investigation. This paper first develops the State Transform Theory (STT), which emphasizes that the problem-solving algorithms are structured according to states and transforms unlike the understanding that underlies traditional surveys which merely emphasize the progress of transforms. The STT, thus, lays the theoretical basis for a new framework for reviewing algorithms. This new construct accommodates the relation-centric algorithms for solving both word and diagrammatic algebra problems. The latter not only highlights the necessity of introducing new states but also allows revelation of contributions of individual algorithms obscured in prior reviews without this approach.

Hologram Reasoning for Solving Algebra Problems with Geometry Diagrams

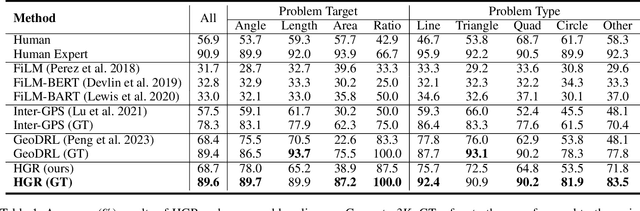
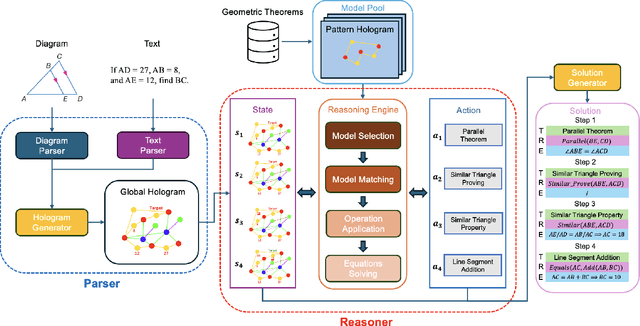
Solving Algebra Problems with Geometry Diagrams (APGDs) is still a challenging problem because diagram processing is not studied as intensively as language processing. To work against this challenge, this paper proposes a hologram reasoning scheme and develops a high-performance method for solving APGDs by using this scheme. To reach this goal, it first defines a hologram, being a kind of graph, and proposes a hologram generator to convert a given APGD into a hologram, which represents the entire information of APGD and the relations for solving the problem can be acquired from it by a uniform way. Then HGR, a hologram reasoning method employs a pool of prepared graph models to derive algebraic equations, which is consistent with the geometric theorems. This method is able to be updated by adding new graph models into the pool. Lastly, it employs deep reinforcement learning to enhance the efficiency of model selection from the pool. The entire HGR not only ensures high solution accuracy with fewer reasoning steps but also significantly enhances the interpretability of the solution process by providing descriptions of all reasoning steps. Experimental results demonstrate the effectiveness of HGR in improving both accuracy and interpretability in solving APGDs.