Enhancing Multirotor Drone Efficiency: Exploring Minimum Energy Consumption Rate of Forward Flight under Varying Payload

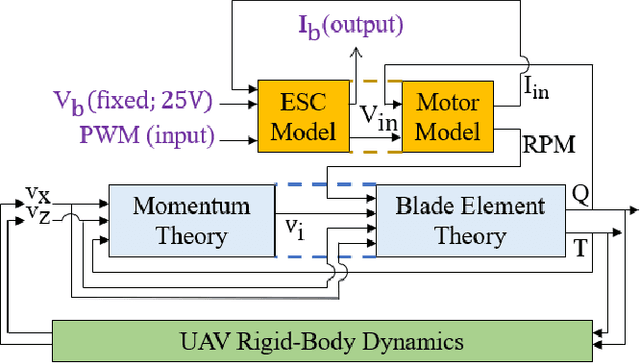
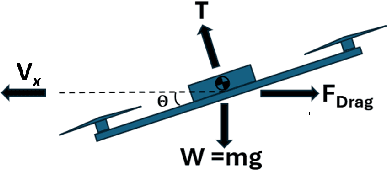
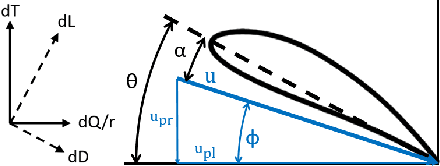
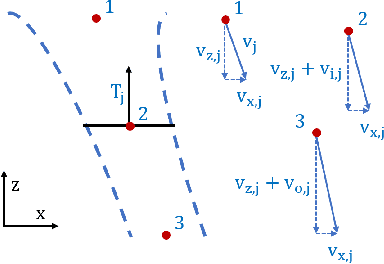
Multirotor unmanned aerial vehicle is a prevailing type of aircraft with wide real-world applications. Energy efficiency is a critical aspect of its performance, determining the range and duration of the missions that can be performed. In this study, we show both analytically and numerically that the optimum of a key energy efficiency index in forward flight, namely energy per meter traveled per unit mass, is a constant under different vehicle mass (including payload). Note that this relationship is only true under the optimal forward velocity that minimizes the energy consumption (under different mass), but not under arbitrary velocity. The study is based on a previously developed model capturing the first-principle energy dynamics of the multirotor, and a key step is to prove that the pitch angle under optimal velocity is a constant. By employing both analytical derivation and validation studies, the research provides critical insights into the optimization of multirotor energy efficiency, and facilitate the development of flight control strategies to extend mission duration and range.

Energy-Optimal Planning of Waypoint-Based UAV Missions -- Does Minimum Distance Mean Minimum Energy?

Multirotor unmanned aerial vehicle is a prevailing type of aerial robots with wide real-world applications. The energy efficiency of the robot is a critical aspect of its performance, determining the range and duration of the missions that can be performed. This paper studies the energy-optimal planning of the multirotor, which aims at finding the optimal ordering of waypoints with the minimum energy consumption for missions in 3D space. The study is performed based on a previously developed model capturing first-principle energy dynamics of the multirotor. We found that in majority of the cases (up to 95%) the solutions of the energy-optimal planning are different from those of the traditional traveling salesman problem which minimizes the total distance. The difference can be as high as 14.9%, with the average at 1.6%-3.3% and 90th percentile at 3.7%-6.5% depending on the range and number of waypoints in the mission. We then identified and explained the key features of the minimum-energy order by correlating to the underlying flight energy dynamics. It is shown that instead of minimizing the distance, coordination of vertical and horizontal motion to promote aerodynamic efficiency is the key to optimizing energy consumption.

Structural Constraints for Physics-augmented Learning

When the physics is wrong, physics-informed machine learning becomes physics-misinformed machine learning. A powerful black-box model should not be able to conceal misconceived physics. We propose two criteria that can be used to assert integrity that a hybrid (physics plus black-box) model: 0) the black-box model should be unable to replicate the physical model, and 1) any best-fit hybrid model has the same physical parameter as a best-fit standalone physics model. We demonstrate them for a sample nonlinear mechanical system approximated by its small-signal linearization.

Finite-sample Identification of Continuous-time Parameter-linear Systems

Differentiating noisy, discrete measurements in order to fit an ordinary differential equation can be unreasonably effective. Assuming square-integrable noise and minimal flow regularity, we construct and analyze a finite-difference differentiation filter and a Tikhonov-regularized least squares estimator for the continuous-time parameter-linear system. Combining these contributions in series, we obtain a finite-sample bound on mean absolute error of estimation. As a by-product, we offer a novel analysis of stochastically perturbed Moore-Penrose pseudoinverses.