Virtual Nodes Improve Long-term Traffic Prediction

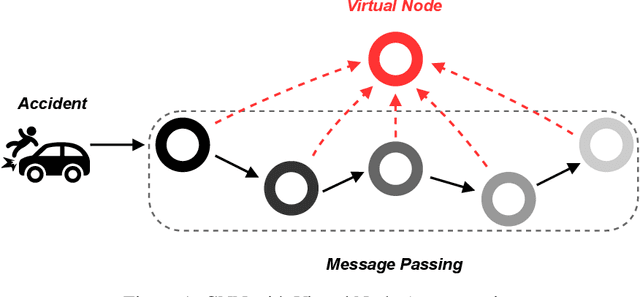
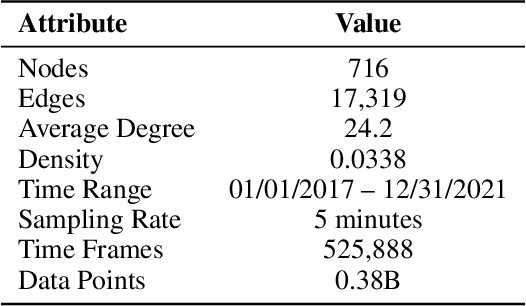
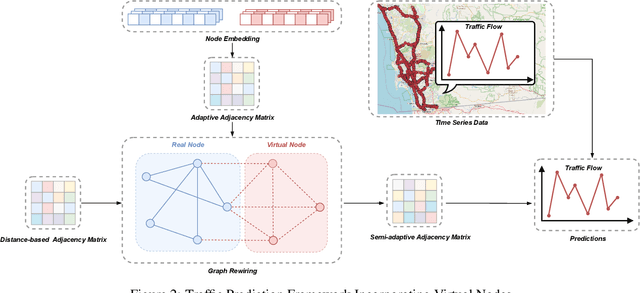
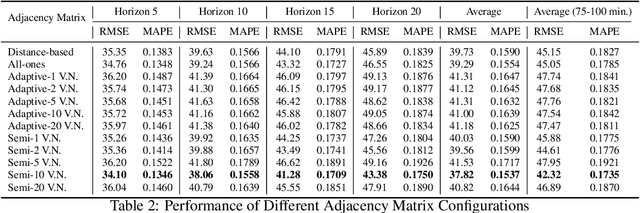
Effective traffic prediction is a cornerstone of intelligent transportation systems, enabling precise forecasts of traffic flow, speed, and congestion. While traditional spatio-temporal graph neural networks (ST-GNNs) have achieved notable success in short-term traffic forecasting, their performance in long-term predictions remains limited. This challenge arises from over-squashing problem, where bottlenecks and limited receptive fields restrict information flow and hinder the modeling of global dependencies. To address these challenges, this study introduces a novel framework that incorporates virtual nodes, which are additional nodes added to the graph and connected to existing nodes, in order to aggregate information across the entire graph within a single GNN layer. Our proposed model incorporates virtual nodes by constructing a semi-adaptive adjacency matrix. This matrix integrates distance-based and adaptive adjacency matrices, allowing the model to leverage geographical information while also learning task-specific features from data. Experimental results demonstrate that the inclusion of virtual nodes significantly enhances long-term prediction accuracy while also improving layer-wise sensitivity to mitigate the over-squashing problem. Virtual nodes also offer enhanced explainability by focusing on key intersections and high-traffic areas, as shown by the visualization of their adjacency matrix weights on road network heat maps. Our advanced approach enhances the understanding and management of urban traffic systems, making it particularly well-suited for real-world applications.

Pareto Control Barrier Function for Inner Safe Set Maximization Under Input Constraints

This article introduces the Pareto Control Barrier Function (PCBF) algorithm to maximize the inner safe set of dynamical systems under input constraints. Traditional Control Barrier Functions (CBFs) ensure safety by maintaining system trajectories within a safe set but often fail to account for realistic input constraints. To address this problem, we leverage the Pareto multi-task learning framework to balance competing objectives of safety and safe set volume. The PCBF algorithm is applicable to high-dimensional systems and is computationally efficient. We validate its effectiveness through comparison with Hamilton-Jacobi reachability for an inverted pendulum and through simulations on a 12-dimensional quadrotor system. Results show that the PCBF consistently outperforms existing methods, yielding larger safe sets and ensuring safety under input constraints.