An ensemble learning framework based on group decision making

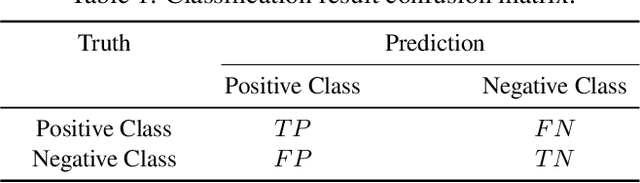
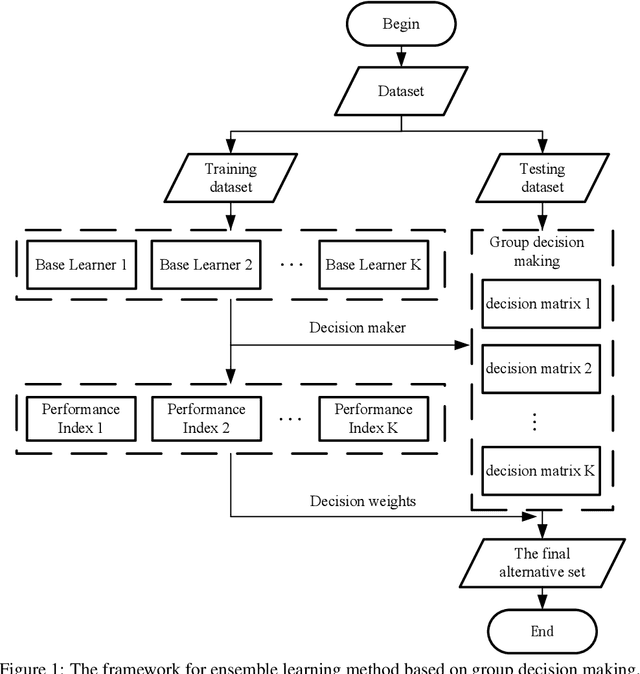
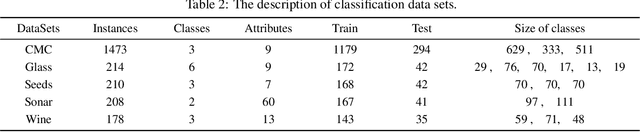
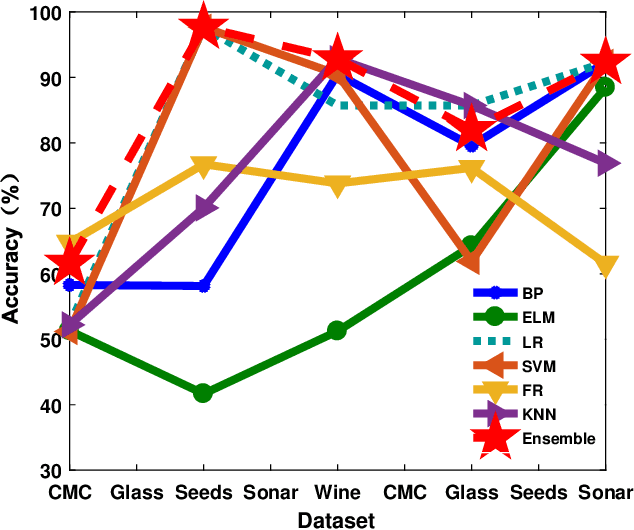
The classification problem is a significant topic in machine learning which aims to teach machines how to group together data by particular criteria. In this paper, a framework for the ensemble learning (EL) method based on group decision making (GDM) has been proposed to resolve this issue. In this framework, base learners can be considered as decision-makers, different categories can be seen as alternatives, classification results obtained by diverse base learners can be considered as performance ratings, and the precision, recall, and accuracy which can reflect the performances of the classification methods can be employed to identify the weights of decision-makers in GDM. Moreover, considering that the precision and recall defined in binary classification problems can not be used directly in the multi-classification problem, the One vs Rest (OvR) has been proposed to obtain the precision and recall of the base learner for each category. The experimental results demonstrate that the proposed EL method based on GDM has higher accuracy than other 6 current popular classification methods in most instances, which verifies the effectiveness of the proposed method.

State Transition Algorithm

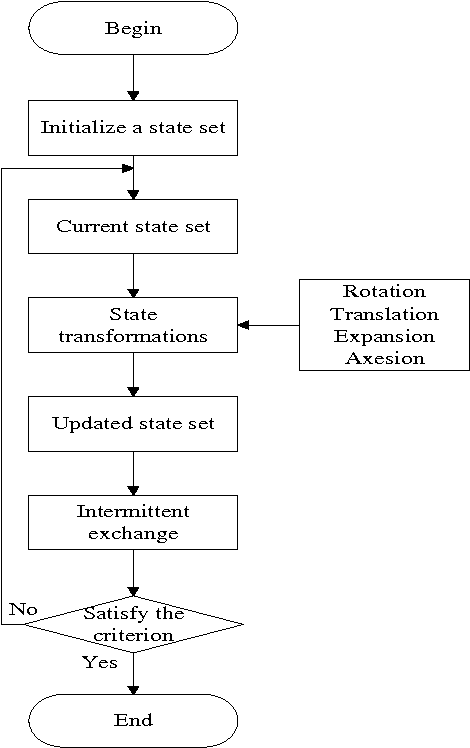
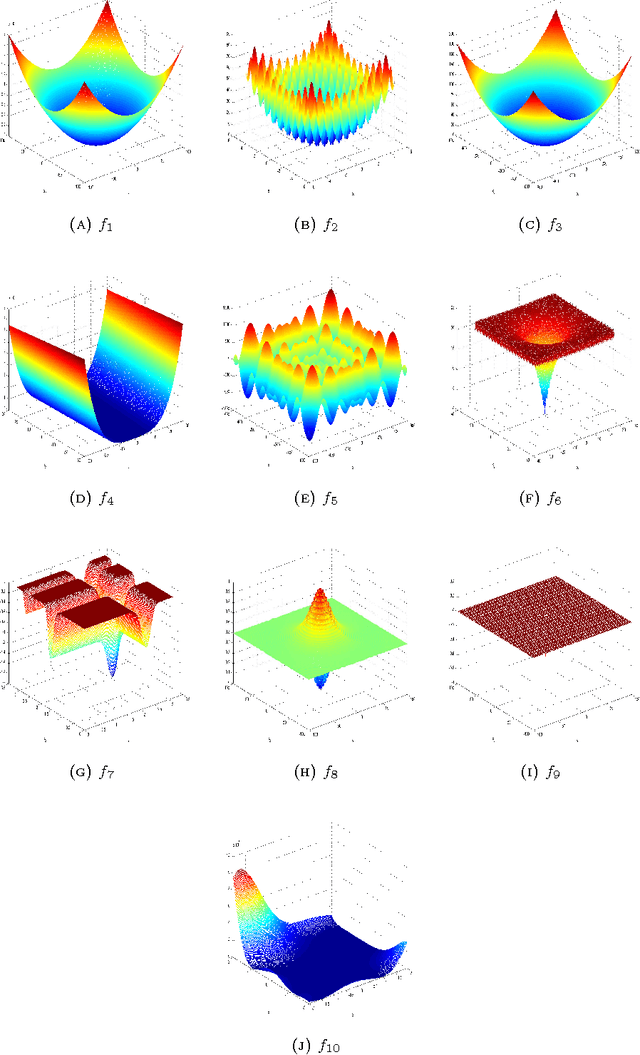
In terms of the concepts of state and state transition, a new heuristic random search algorithm named state transition algorithm is proposed. For continuous function optimization problems, four special transformation operators called rotation, translation, expansion and axesion are designed. Adjusting measures of the transformations are mainly studied to keep the balance of exploration and exploitation. Convergence analysis is also discussed about the algorithm based on random search theory. In the meanwhile, to strengthen the search ability in high dimensional space, communication strategy is introduced into the basic algorithm and intermittent exchange is presented to prevent premature convergence. Finally, experiments are carried out for the algorithms. With 10 common benchmark unconstrained continuous functions used to test the performance, the results show that state transition algorithms are promising algorithms due to their good global search capability and convergence property when compared with some popular algorithms.

A Discrete State Transition Algorithm for Generalized Traveling Salesman Problem

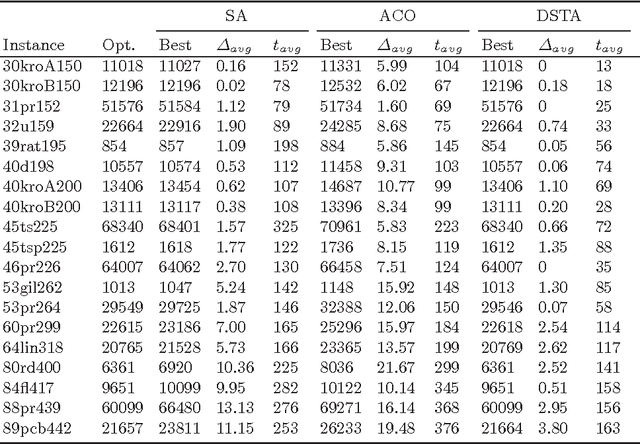
Generalized traveling salesman problem (GTSP) is an extension of classical traveling salesman problem (TSP), which is a combinatorial optimization problem and an NP-hard problem. In this paper, an efficient discrete state transition algorithm (DSTA) for GTSP is proposed, where a new local search operator named \textit{K-circle}, directed by neighborhood information in space, has been introduced to DSTA to shrink search space and strengthen search ability. A novel robust update mechanism, restore in probability and risk in probability (Double R-Probability), is used in our work to escape from local minima. The proposed algorithm is tested on a set of GTSP instances. Compared with other heuristics, experimental results have demonstrated the effectiveness and strong adaptability of DSTA and also show that DSTA has better search ability than its competitors.

Initial Version of State Transition Algorithm

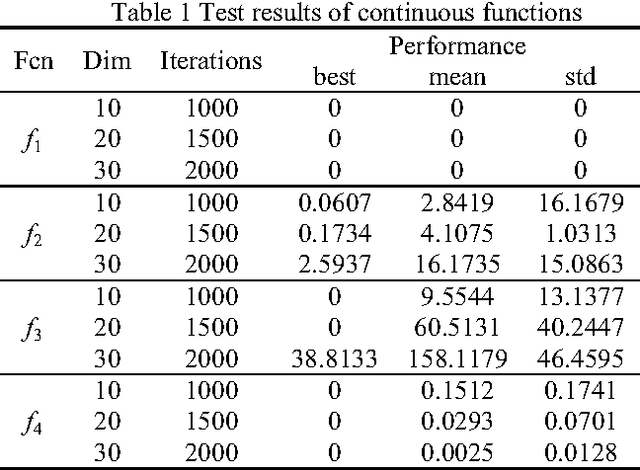
In terms of the concepts of state and state transition, a new algorithm-State Transition Algorithm (STA) is proposed in order to probe into classical and intelligent optimization algorithms. On the basis of state and state transition, it becomes much simpler and easier to understand. As for continuous function optimization problems, three special operators named rotation, translation and expansion are presented. While for discrete function optimization problems, an operator called general elementary transformation is introduced. Finally, with 4 common benchmark continuous functions and a discrete problem used to test the performance of STA, the experiment shows that STA is a promising algorithm due to its good search capability.