Xiao-Ping Wang
A Fast Algorithm for Geodesic Active Contours with Applications to Medical Image Segmentation
Jul 01, 2020
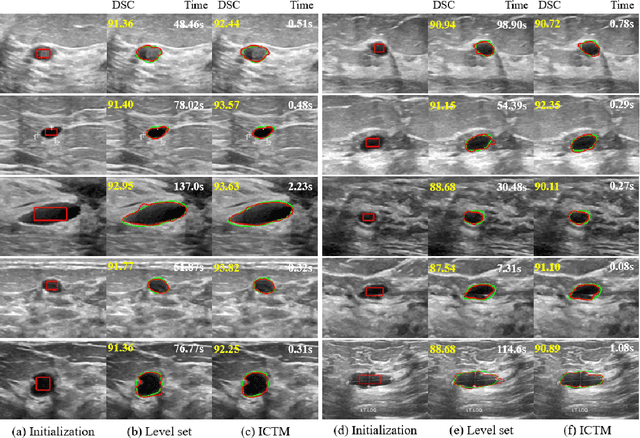
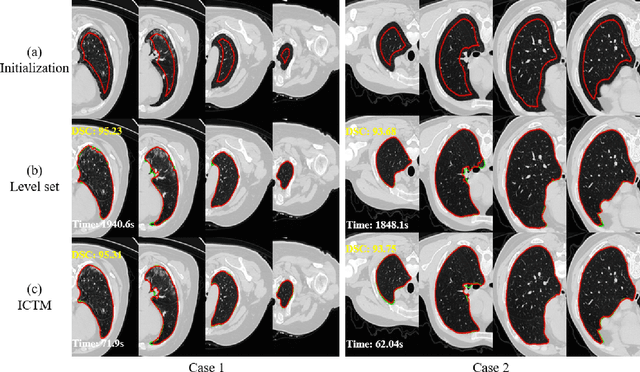
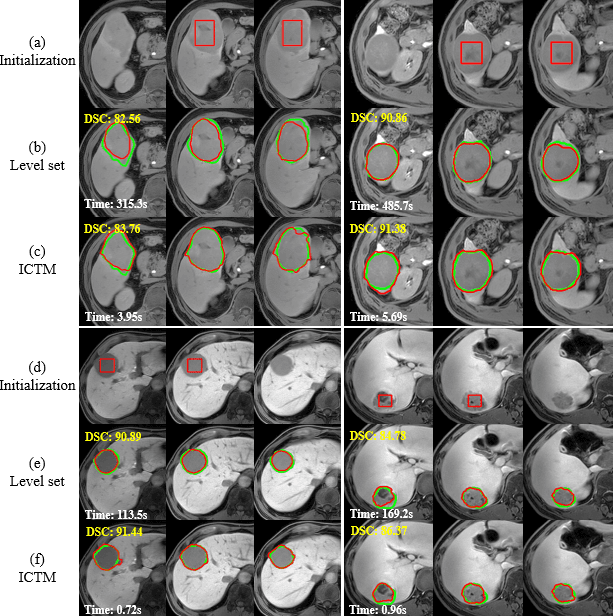
Abstract:The geodesic active contour model (GAC) is a commonly used segmentation model for medical image segmentation. The level set method (LSM) is the most popular approach for solving the model, via implicitly representing the contour by a level set function. However, the LSM suffers from high computation burden and numerical instability, requiring additional regularization terms or re-initialization techniques. In this paper, we use characteristic functions to implicitly approximate the contours, propose a new representation to the GAC and derive an efficient algorithm termed as the iterative convolution-thresholding method (ICTM). Compared to the LSM, the ICTM is simpler and much more efficient and stable. In addition, the ICTM enjoys most desired features (e.g., topological changes) of the level set-based methods. Extensive experiments, on 2D synthetic, 2D ultrasound, 3D CT, and 3D MR images for nodule, organ and lesion segmentation, demonstrate that the ICTM not only obtains comparable or even better segmentation results (compared to the LSM) but also achieves dozens or hundreds of times acceleration.
The iterative convolution-thresholding method (ICTM) for image segmentation
Apr 24, 2019
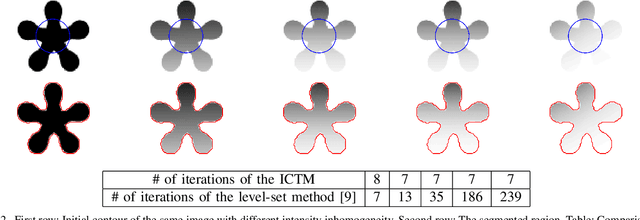


Abstract:In this paper, we propose a novel iterative convolution-thresholding method (ICTM) that is applicable to a range of variational models for image segmentation. A variational model usually minimizes an energy functional consisting of a fidelity term and a regularization term. In the ICTM, the interface between two different segment domains is implicitly represented by their characteristic functions. The fidelity term is then usually written as a linear functional of the characteristic functions and the regularized term is approximated by a functional of characteristic functions in terms of heat kernel convolution. This allows us to design an iterative convolution-thresholding method to minimize the approximate energy. The method is simple, efficient and enjoys the energy-decaying property. Numerical experiments show that the method is easy to implement, robust and applicable to various image segmentation models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge