BELIEF in Dependence: Leveraging Atomic Linearity in Data Bits for Rethinking Generalized Linear Models

Two linearly uncorrelated binary variables must be also independent because non-linear dependence cannot manifest with only two possible states. This inherent linearity is the atom of dependency constituting any complex form of relationship. Inspired by this observation, we develop a framework called binary expansion linear effect (BELIEF) for assessing and understanding arbitrary relationships with a binary outcome. Models from the BELIEF framework are easily interpretable because they describe the association of binary variables in the language of linear models, yielding convenient theoretical insight and striking parallels with the Gaussian world. In particular, an algebraic structure on the predictors with nonzero slopes governs conditional independence properties. With BELIEF, one may study generalized linear models (GLM) through transparent linear models, providing insight into how modeling is affected by the choice of link. For example, setting a GLM interaction coefficient to zero does not necessarily lead to the kind of no-interaction model assumption as understood under their linear model counterparts. Furthermore, for a binary response, maximum likelihood estimation for GLMs paradoxically fails under complete separation, when the data are most discriminative, whereas BELIEF estimation automatically reveals the perfect predictor in the data that is responsible for complete separation. We explore these phenomena and provide a host of related theoretical results. We also provide preliminary empirical demonstration and verification of some theoretical results.

Scalable Spike-and-Slab

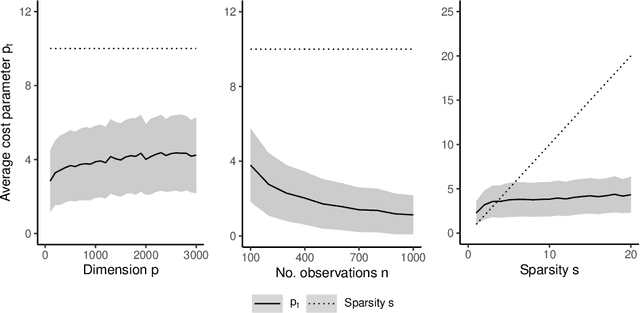
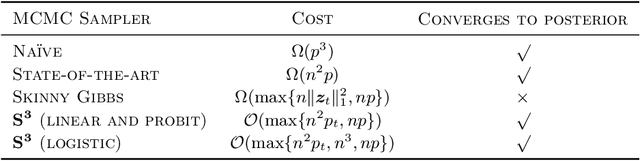
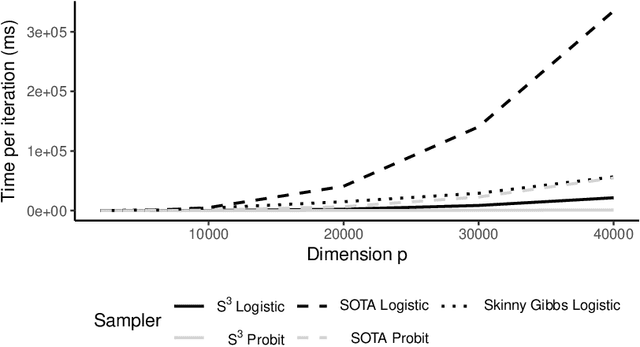
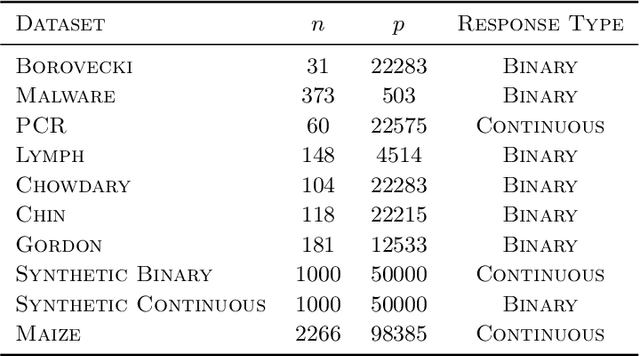
Spike-and-slab priors are commonly used for Bayesian variable selection, due to their interpretability and favorable statistical properties. However, existing samplers for spike-and-slab posteriors incur prohibitive computational costs when the number of variables is large. In this article, we propose Scalable Spike-and-Slab ($S^3$), a scalable Gibbs sampling implementation for high-dimensional Bayesian regression with the continuous spike-and-slab prior of George and McCulloch (1993). For a dataset with $n$ observations and $p$ covariates, $S^3$ has order $\max\{ n^2 p_t, np \}$ computational cost at iteration $t$ where $p_t$ never exceeds the number of covariates switching spike-and-slab states between iterations $t$ and $t-1$ of the Markov chain. This improves upon the order $n^2 p$ per-iteration cost of state-of-the-art implementations as, typically, $p_t$ is substantially smaller than $p$. We apply $S^3$ on synthetic and real-world datasets, demonstrating orders of magnitude speed-ups over existing exact samplers and significant gains in inferential quality over approximate samplers with comparable cost.