Scalable Spike-and-Slab

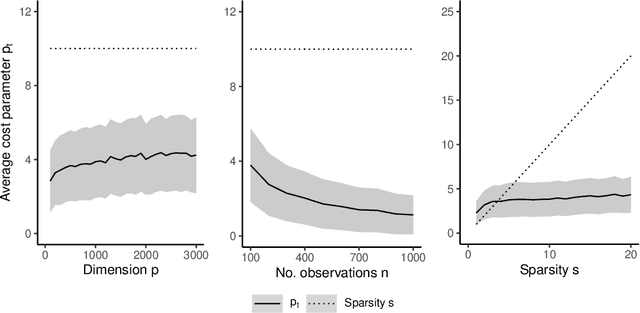
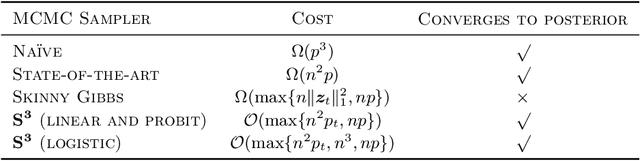
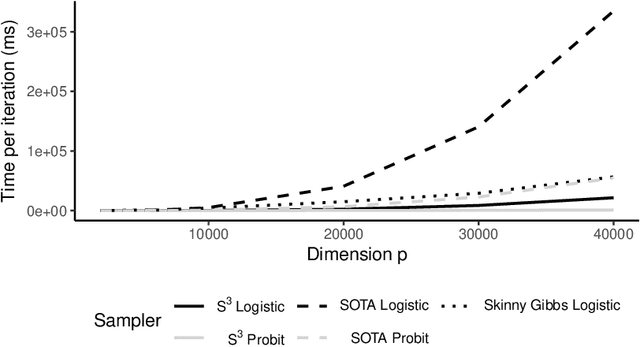
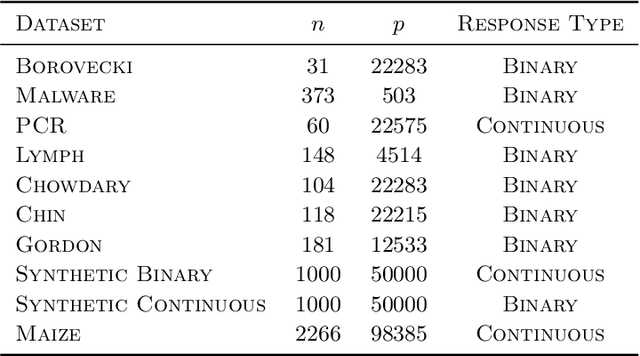
Spike-and-slab priors are commonly used for Bayesian variable selection, due to their interpretability and favorable statistical properties. However, existing samplers for spike-and-slab posteriors incur prohibitive computational costs when the number of variables is large. In this article, we propose Scalable Spike-and-Slab ($S^3$), a scalable Gibbs sampling implementation for high-dimensional Bayesian regression with the continuous spike-and-slab prior of George and McCulloch (1993). For a dataset with $n$ observations and $p$ covariates, $S^3$ has order $\max\{ n^2 p_t, np \}$ computational cost at iteration $t$ where $p_t$ never exceeds the number of covariates switching spike-and-slab states between iterations $t$ and $t-1$ of the Markov chain. This improves upon the order $n^2 p$ per-iteration cost of state-of-the-art implementations as, typically, $p_t$ is substantially smaller than $p$. We apply $S^3$ on synthetic and real-world datasets, demonstrating orders of magnitude speed-ups over existing exact samplers and significant gains in inferential quality over approximate samplers with comparable cost.

Bounding Wasserstein distance with couplings

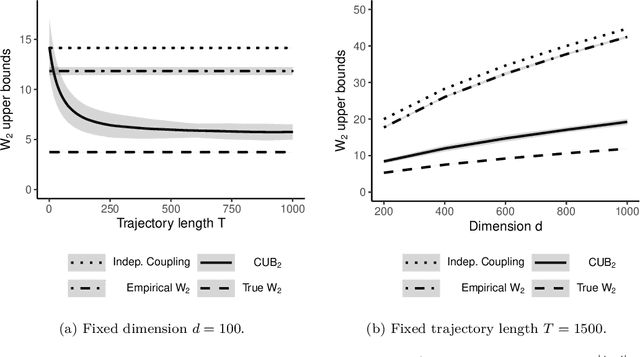
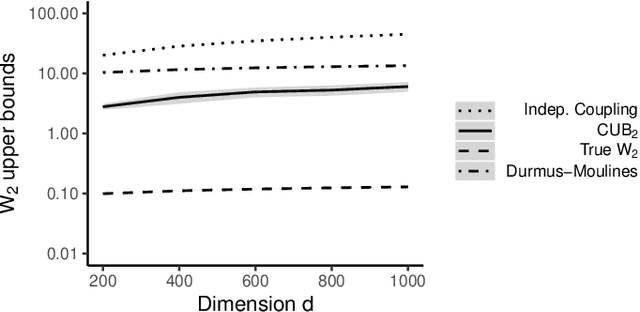
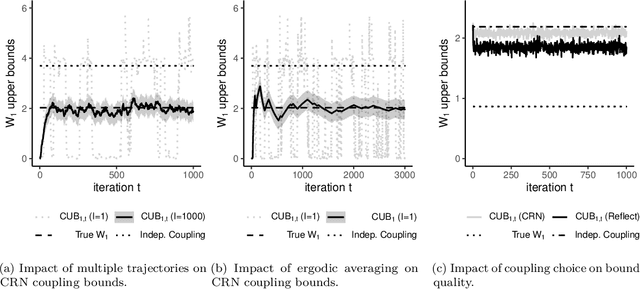
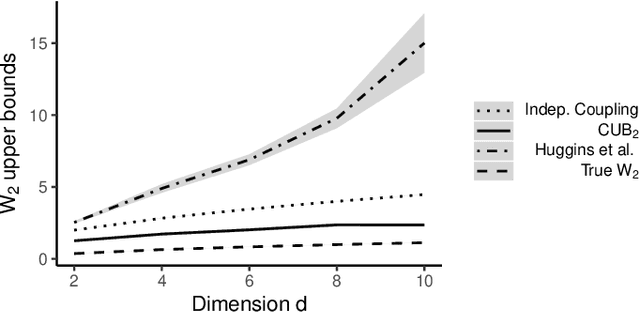
Markov chain Monte Carlo (MCMC) provides asymptotically consistent estimates of intractable posterior expectations as the number of iterations tends to infinity. However, in large data applications, MCMC can be computationally expensive per iteration. This has catalyzed interest in sampling methods such as approximate MCMC, which trade off asymptotic consistency for improved computational speed. In this article, we propose estimators based on couplings of Markov chains to assess the quality of such asymptotically biased sampling methods. The estimators give empirical upper bounds of the Wassertein distance between the limiting distribution of the asymptotically biased sampling method and the original target distribution of interest. We establish theoretical guarantees for our upper bounds and show that our estimators can remain effective in high dimensions. We apply our quality measures to stochastic gradient MCMC, variational Bayes, and Laplace approximations for tall data and to approximate MCMC for Bayesian logistic regression in 4500 dimensions and Bayesian linear regression in 50000 dimensions.