Global Consistent Point Cloud Registration Based on Lie-algebraic Cohomology

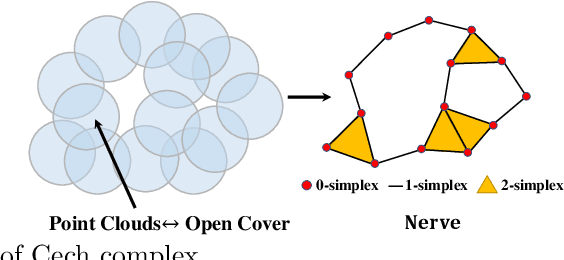
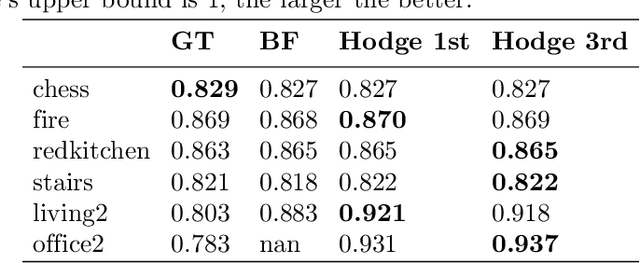
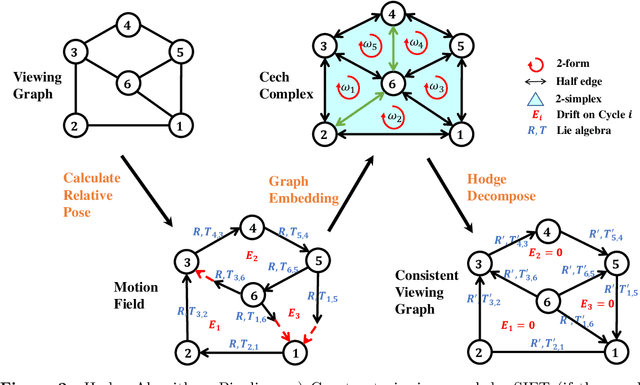
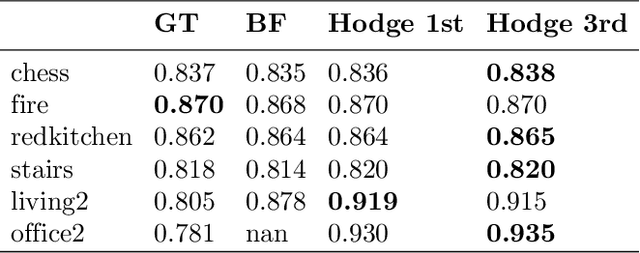
We present a novel, effective method for global point cloud registration problems by geometric topology. Based on many point cloud pairwise registration methods (e.g ICP), we focus on the problem of accumulated error for the composition of transformations along any loops. The major technical contribution of this paper is a linear method for the elimination of errors, using only solving a Poisson equation. We demonstrate the consistency of our method from Hodge-Helmhotz decomposition theorem and experiments on multiple RGBD datasets of real-world scenes. The experimental results also demonstrate that our global registration method runs quickly and provides accurate reconstructions.

Robot Coverage Path Planning for General Surfaces Using Quadratic Differentials

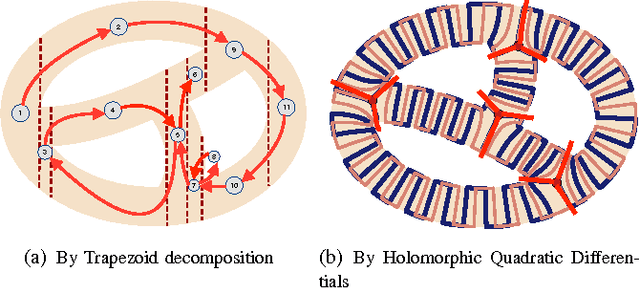
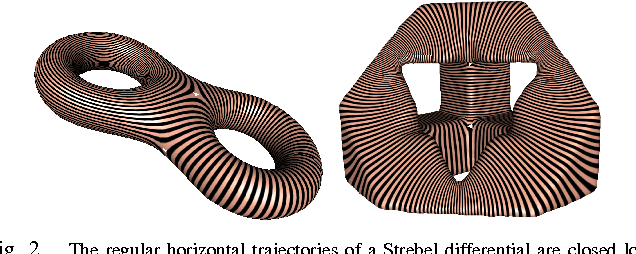
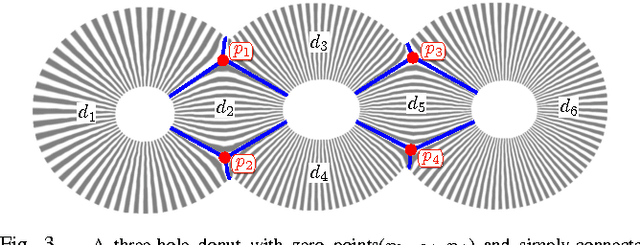
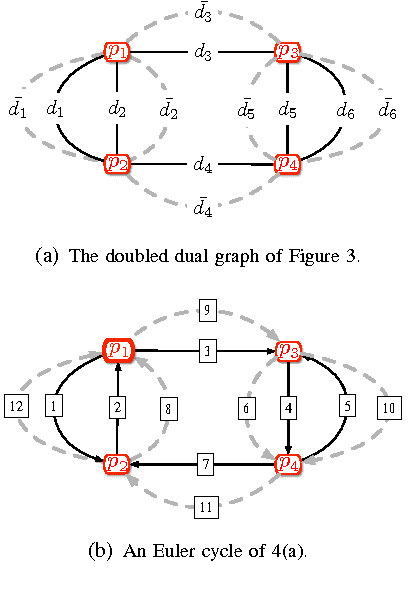
Robot Coverage Path planning (i.e., provide full coverage of a given domain by one or multiple robots) is a classical problem in the field of robotics and motion planning. The goal is to provide nearly full coverage while also minimize duplicately visited area. In this paper we focus on the scenario of path planning on general surfaces including planar domains with complex topology, complex terrain or general surface in 3D space. The main idea is to adopt a natural, intrinsic and global parametrization of the surface for robot path planning, namely the holomorphic quadratic differentials. Except for a small number of zero points (singularities), each point on the surface is given a uv-coordinates naturally represented by a complex number. We show that natural, efficient robot paths can be obtained by using such coordinate systems. The method is based on intrinsic geometry and thus can be adapted to general surface exploration in 3D.