Policy Gradient Methods for Risk-Sensitive Distributional Reinforcement Learning with Provable Convergence

Risk-sensitive reinforcement learning (RL) is crucial for maintaining reliable performance in many high-stakes applications. While most RL methods aim to learn a point estimate of the random cumulative cost, distributional RL (DRL) seeks to estimate the entire distribution of it. The distribution provides all necessary information about the cost and leads to a unified framework for handling various risk measures in a risk-sensitive setting. However, developing policy gradient methods for risk-sensitive DRL is inherently more complex as it pertains to finding the gradient of a probability measure. This paper introduces a policy gradient method for risk-sensitive DRL with general coherent risk measures, where we provide an analytical form of the probability measure's gradient. We further prove the local convergence of the proposed algorithm under mild smoothness assumptions. For practical use, we also design a categorical distributional policy gradient algorithm (CDPG) based on categorical distributional policy evaluation and trajectory-based gradient estimation. Through experiments on a stochastic cliff-walking environment, we illustrate the benefits of considering a risk-sensitive setting in DRL.

On the Global Convergence of Risk-Averse Policy Gradient Methods with Dynamic Time-Consistent Risk Measures

Risk-sensitive reinforcement learning (RL) has become a popular tool to control the risk of uncertain outcomes and ensure reliable performance in various sequential decision-making problems. While policy gradient methods have been developed for risk-sensitive RL, it remains unclear if these methods enjoy the same global convergence guarantees as in the risk-neutral case. In this paper, we consider a class of dynamic time-consistent risk measures, called Expected Conditional Risk Measures (ECRMs), and derive policy gradient updates for ECRM-based objective functions. Under both constrained direct parameterization and unconstrained softmax parameterization, we provide global convergence of the corresponding risk-averse policy gradient algorithms. We further test a risk-averse variant of REINFORCE algorithm on a stochastic Cliffwalk environment to demonstrate the efficacy of our algorithm and the importance of risk control.

Risk-Averse Reinforcement Learning via Dynamic Time-Consistent Risk Measures

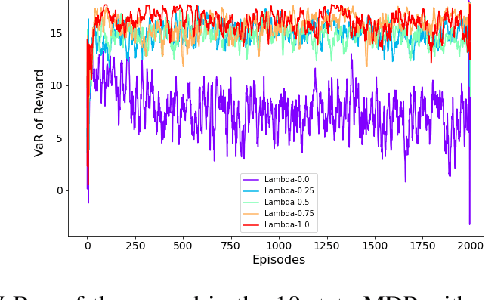
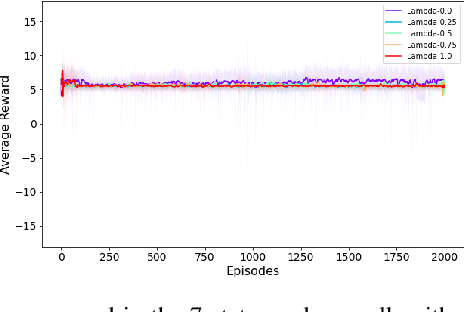
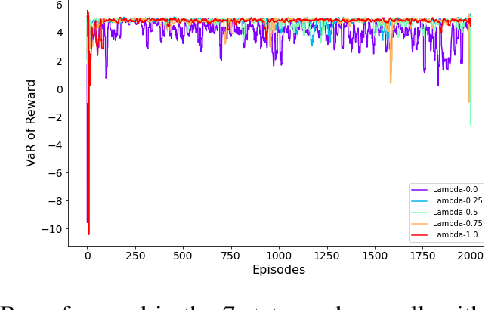
Traditional reinforcement learning (RL) aims to maximize the expected total reward, while the risk of uncertain outcomes needs to be controlled to ensure reliable performance in a risk-averse setting. In this paper, we consider the problem of maximizing dynamic risk of a sequence of rewards in infinite-horizon Markov Decision Processes (MDPs). We adapt the Expected Conditional Risk Measures (ECRMs) to the infinite-horizon risk-averse MDP and prove its time consistency. Using a convex combination of expectation and conditional value-at-risk (CVaR) as a special one-step conditional risk measure, we reformulate the risk-averse MDP as a risk-neutral counterpart with augmented action space and manipulation on the immediate rewards. We further prove that the related Bellman operator is a contraction mapping, which guarantees the convergence of any value-based RL algorithms. Accordingly, we develop a risk-averse deep Q-learning framework, and our numerical studies based on two simple MDPs show that the risk-averse setting can reduce the variance and enhance robustness of the results.