Xenophon Chatzigeorgiou
Efficiency and complexity of price competition among single-product vendors
Mar 06, 2017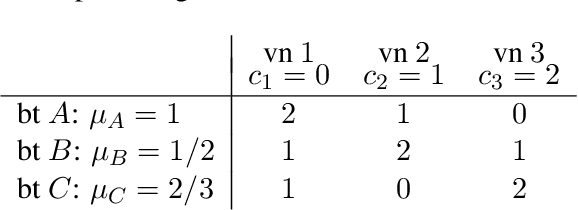
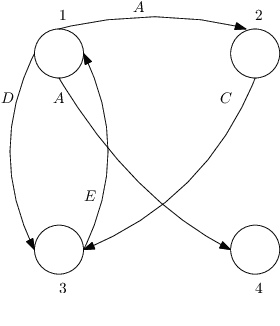
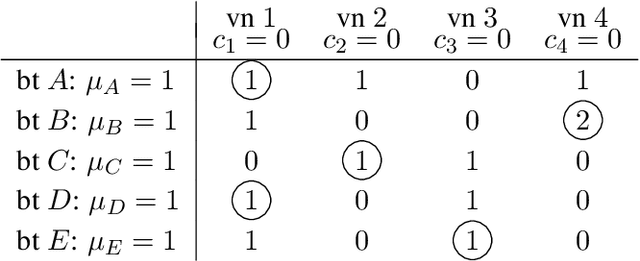
Abstract:Motivated by recent progress on pricing in the AI literature, we study marketplaces that contain multiple vendors offering identical or similar products and unit-demand buyers with different valuations on these vendors. The objective of each vendor is to set the price of its product to a fixed value so that its profit is maximized. The profit depends on the vendor's price itself and the total volume of buyers that find the particular price more attractive than the price of the vendor's competitors. We model the behaviour of buyers and vendors as a two-stage full-information game and study a series of questions related to the existence, efficiency (price of anarchy) and computational complexity of equilibria in this game. To overcome situations where equilibria do not exist or exist but are highly inefficient, we consider the scenario where some of the vendors are subsidized in order to keep prices low and buyers highly satisfied.
Optimizing positional scoring rules for rank aggregation
Sep 18, 2016


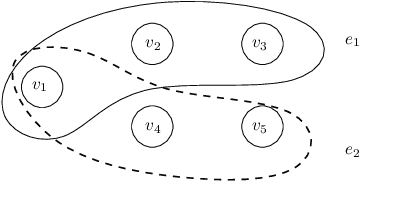
Abstract:Nowadays, several crowdsourcing projects exploit social choice methods for computing an aggregate ranking of alternatives given individual rankings provided by workers. Motivated by such systems, we consider a setting where each worker is asked to rank a fixed (small) number of alternatives and, then, a positional scoring rule is used to compute the aggregate ranking. Among the apparently infinite such rules, what is the best one to use? To answer this question, we assume that we have partial access to an underlying true ranking. Then, the important optimization problem to be solved is to compute the positional scoring rule whose outcome, when applied to the profile of individual rankings, is as close as possible to the part of the underlying true ranking we know. We study this fundamental problem from a theoretical viewpoint and present positive and negative complexity results and, furthermore, complement our theoretical findings with experiments on real-world and synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge