Evaluating approval-based multiwinner voting in terms of robustness to noise

Approval-based multiwinner voting rules have recently received much attention in the Computational Social Choice literature. Such rules aggregate approval ballots and determine a winning committee of alternatives. To assess effectiveness, we propose to employ new noise models that are specifically tailored for approval votes and committees. These models take as input a ground truth committee and return random approval votes to be thought of as noisy estimates of the ground truth. A minimum robustness requirement for an approval-based multiwinner voting rule is to return the ground truth when applied to profiles with sufficiently many noisy votes. Our results indicate that approval-based multiwinner voting is always robust to reasonable noise. We further refine this finding by presenting a hierarchy of rules in terms of how robust to noise they are.

Efficiency and complexity of price competition among single-product vendors

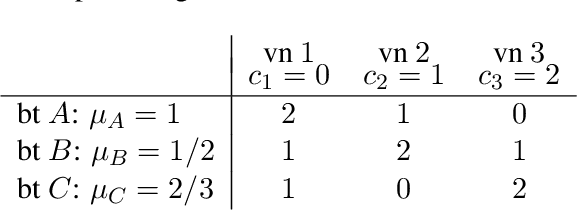
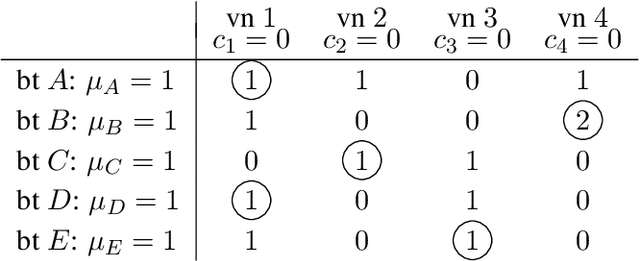
Motivated by recent progress on pricing in the AI literature, we study marketplaces that contain multiple vendors offering identical or similar products and unit-demand buyers with different valuations on these vendors. The objective of each vendor is to set the price of its product to a fixed value so that its profit is maximized. The profit depends on the vendor's price itself and the total volume of buyers that find the particular price more attractive than the price of the vendor's competitors. We model the behaviour of buyers and vendors as a two-stage full-information game and study a series of questions related to the existence, efficiency (price of anarchy) and computational complexity of equilibria in this game. To overcome situations where equilibria do not exist or exist but are highly inefficient, we consider the scenario where some of the vendors are subsidized in order to keep prices low and buyers highly satisfied.

Optimizing positional scoring rules for rank aggregation

Nowadays, several crowdsourcing projects exploit social choice methods for computing an aggregate ranking of alternatives given individual rankings provided by workers. Motivated by such systems, we consider a setting where each worker is asked to rank a fixed (small) number of alternatives and, then, a positional scoring rule is used to compute the aggregate ranking. Among the apparently infinite such rules, what is the best one to use? To answer this question, we assume that we have partial access to an underlying true ranking. Then, the important optimization problem to be solved is to compute the positional scoring rule whose outcome, when applied to the profile of individual rankings, is as close as possible to the part of the underlying true ranking we know. We study this fundamental problem from a theoretical viewpoint and present positive and negative complexity results and, furthermore, complement our theoretical findings with experiments on real-world and synthetic data.

How effective can simple ordinal peer grading be?

Ordinal peer grading has been proposed as a simple and scalable solution for computing reliable information about student performance in massive open online courses. The idea is to outsource the grading task to the students themselves as follows. After the end of an exam, each student is asked to rank ---in terms of quality--- a bundle of exam papers by fellow students. An aggregation rule will then combine the individual rankings into a global one that contains all students. We define a broad class of simple aggregation rules and present a theoretical framework for assessing their effectiveness. When statistical information about the grading behaviour of students is available, the framework can be used to compute the optimal rule from this class with respect to a series of performance objectives. For example, a natural rule known as Borda is proved to be optimal when students grade correctly. In addition, we present extensive simulations and a field experiment that validate our theory and prove it to be extremely accurate in predicting the performance of aggregation rules even when only rough information about grading behaviour is available.

Aggregating partial rankings with applications to peer grading in massive online open courses

We investigate the potential of using ordinal peer grading for the evaluation of students in massive online open courses (MOOCs). According to such grading schemes, each student receives a few assignments (by other students) which she has to rank. Then, a global ranking (possibly translated into numerical scores) is produced by combining the individual ones. This is a novel application area for social choice concepts and methods where the important problem to be solved is as follows: how should the assignments be distributed so that the collected individual rankings can be easily merged into a global one that is as close as possible to the ranking that represents the relative performance of the students in the assignment? Our main theoretical result suggests that using very simple ways to distribute the assignments so that each student has to rank only $k$ of them, a Borda-like aggregation method can recover a $1-O(1/k)$ fraction of the true ranking when each student correctly ranks the assignments she receives. Experimental results strengthen our analysis further and also demonstrate that the same method is extremely robust even when students have imperfect capabilities as graders. We believe that our results provide strong evidence that ordinal peer grading can be a highly effective and scalable solution for evaluation in MOOCs.