Exploration into Optimal State Estimation with Event-triggered Communication

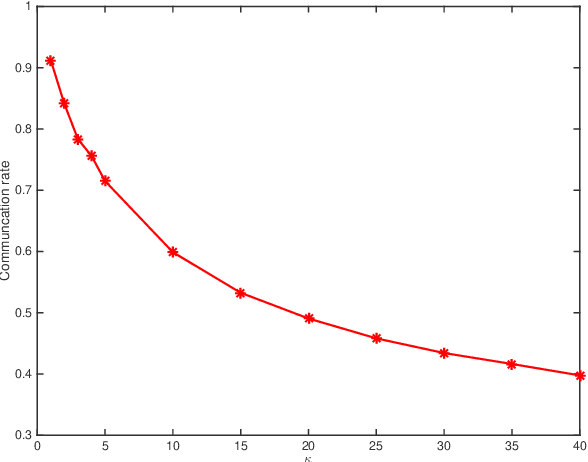
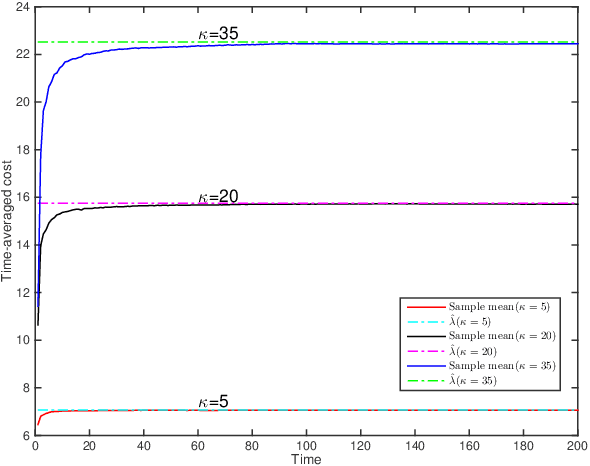
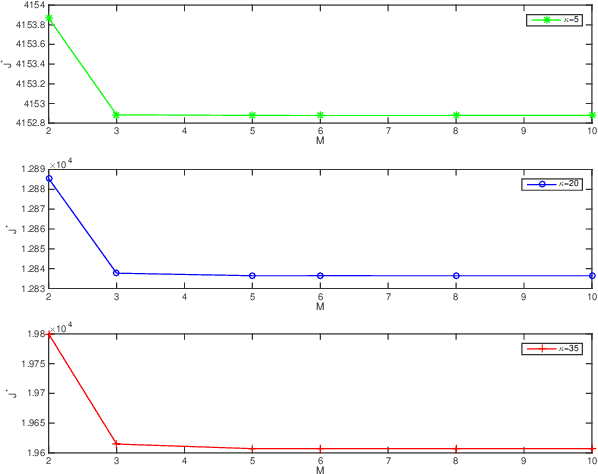
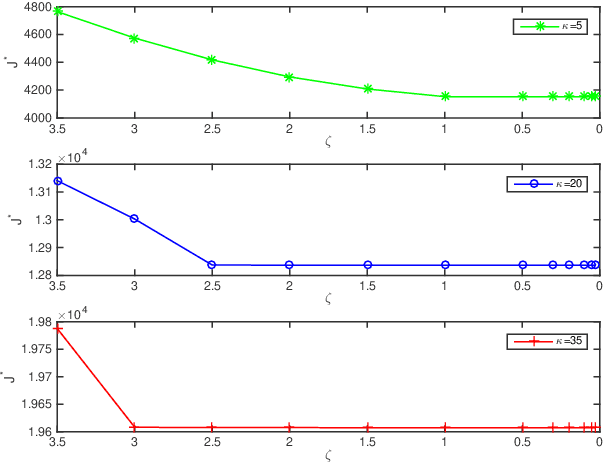
This paper deals with the problem of remote estimation of the state of a discrete-time stochastic linear system observed by a sensor with computational capacity to calculate local estimates. We design an event-triggered communication (ETC) scheme and a remote state estimator to optimally calibrate the tradeoff between system performance and limited communication resources. The novel communication scheme is the time-varying thresholding version for the cumulative innovation-driven communication scheme in [1], and its transmission probability is given. We derive the corresponding remote minimum mean square error (MMSE) estimator and present a tight upper bound for its MSE matrices. We also show that by employing a couple of weak assumptions, the optimality problem becomes (asymptotically) exact and can be addressed in an Markov Decision Process (MDP) framework, which delivers optimal policy and cost in an algorithmic procedure. The simulation results illustrate the effectiveness of our approach.

Guidance Trajectory Mathematical Modeling

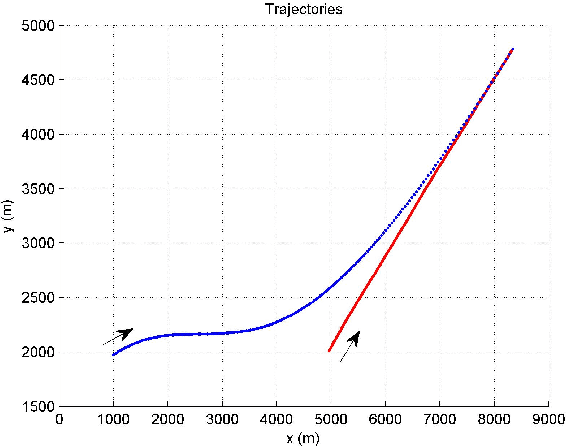
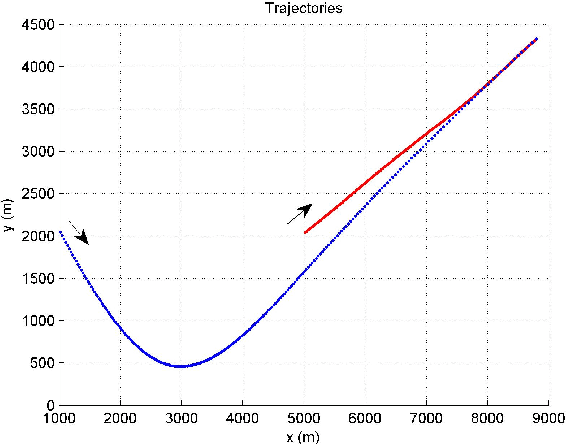
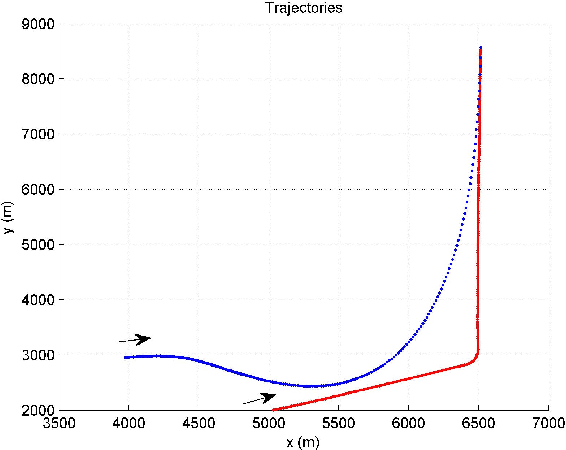
A trajectory of a destination-directed moving object (e.g. an aircraft from an origin airport to a destination airport) has three main components: an origin, a destination, and motion in between. We call such a trajectory that end up at the destination \textit{destination-directed trajectory (DDT)}. A class of conditionally Markov (CM) sequences (called CM$_\text{L}$) has the following main components: a joint density of two endpoints and a Markov-like evolution law. A CM$_\text{L}$ dynamic model can describe the evolution of a DDT but not of a guided object chasing a moving guide. The trajectory of a guided object is called a \textit{guided trajectory (GT)}. Inspired by a CM$_\text{L}$ model, this paper proposes a model for a GT with a moving guide. The proposed model reduces to a CM$_\text{L}$ model if the guide is not moving. We also study filtering and trajectory prediction based on the proposed model. Simulation results are presented.

Gaussian Conditionally Markov Sequences: Dynamic Models and Representations of Reciprocal and Other Classes

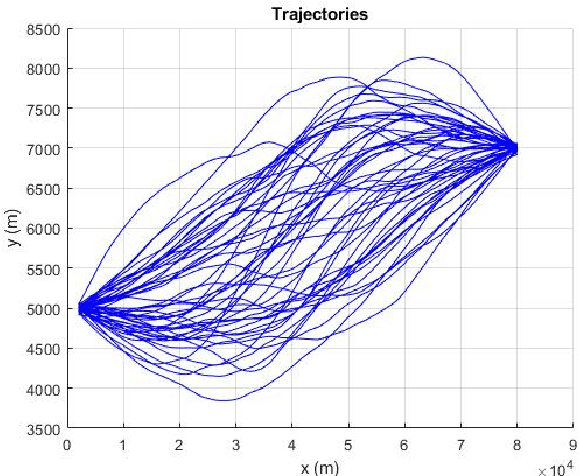
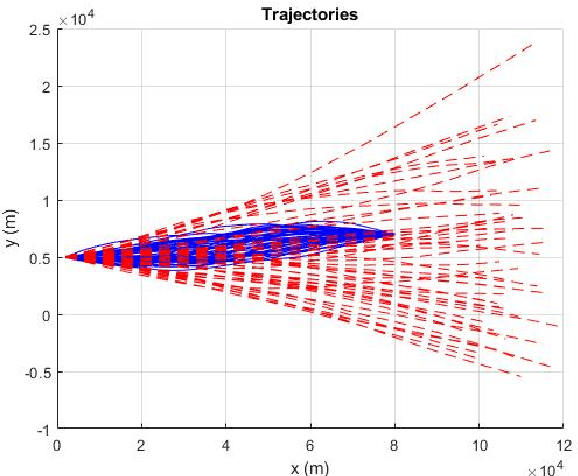
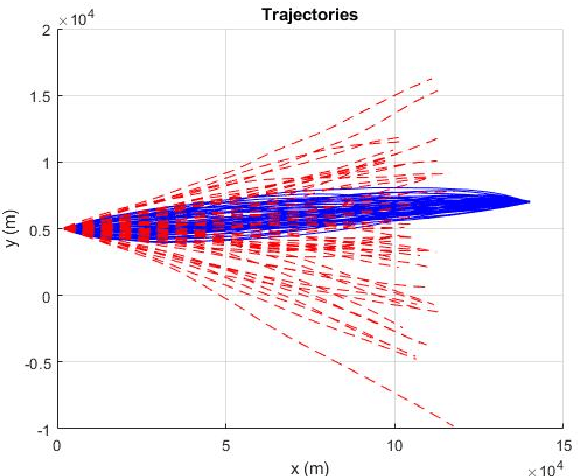
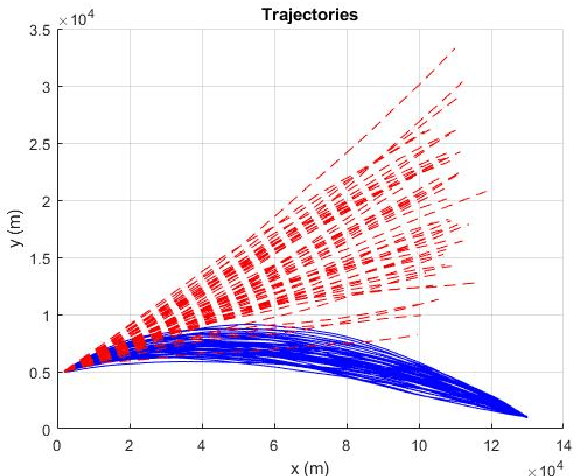
Conditionally Markov (CM) sequences are powerful mathematical tools for modeling problems. One class of CM sequences is the reciprocal sequence. In application, we need not only CM dynamic models, but also know how to design model parameters. Models of two important classes of nonsingular Gaussian (NG) CM sequences, called $CM_L$ and $CM_F$ models, and a model of the NG reciprocal sequence, called reciprocal $CM_L$ model, were presented in our previous works and their applications were discussed. In this paper, these models are studied in more detail, in particular their parameter design. It is shown that every reciprocal $CM_L$ model can be induced by a Markov model. Then, parameters of each reciprocal $CM_L$ model can be obtained from those of the Markov model. Also, it is shown that a NG $CM_L$ ($CM_F$) sequence can be represented by a sum of a NG Markov sequence and an uncorrelated NG vector. This (necessary and sufficient) representation provides a basis for designing parameters of a $CM_L$ ($CM_F$) model. From the CM viewpoint, a representation is also obtained for NG reciprocal sequences. This representation is simple and reveals an important property of reciprocal sequences. As a result, the significance of studying reciprocal sequences from the CM viewpoint is demonstrated. A full spectrum of dynamic models from a $CM_L$ model to a reciprocal $CM_L$ model is also presented. Some examples are presented for illustration.