Gaussian Conditionally Markov Sequences: Dynamic Models and Representations of Reciprocal and Other Classes

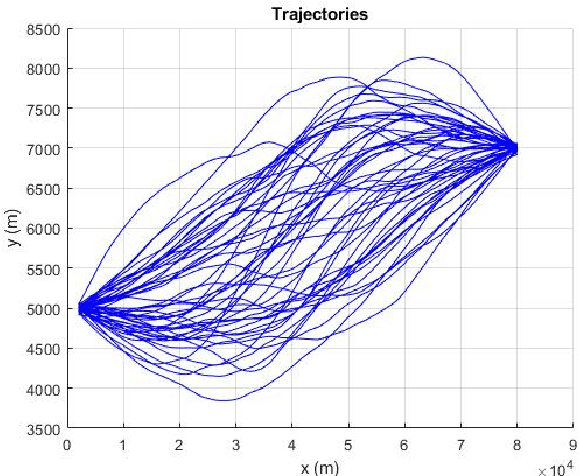
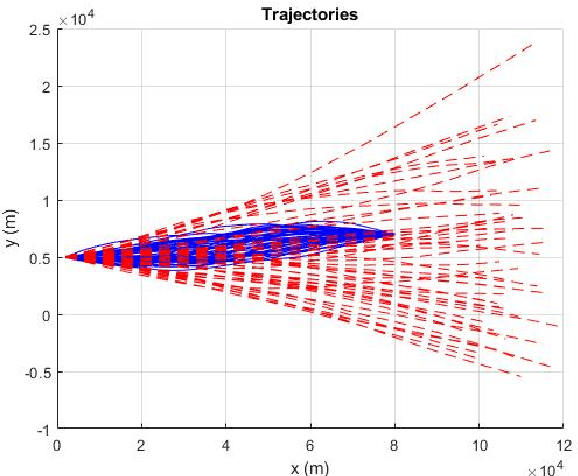
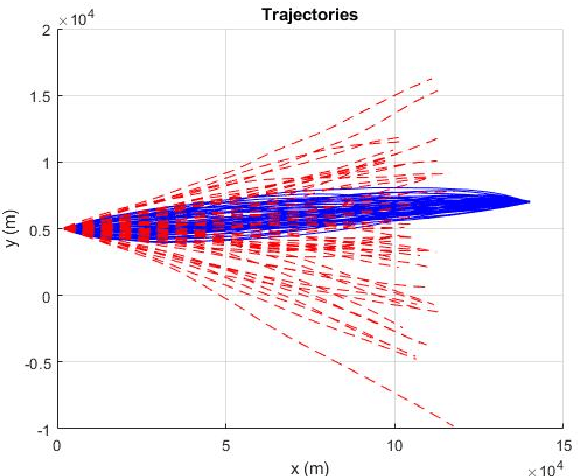
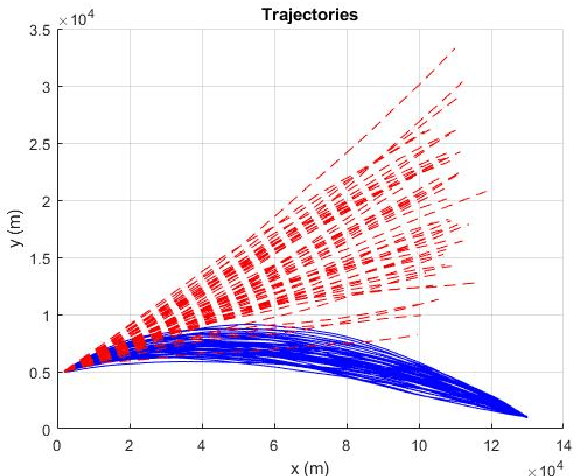
Conditionally Markov (CM) sequences are powerful mathematical tools for modeling problems. One class of CM sequences is the reciprocal sequence. In application, we need not only CM dynamic models, but also know how to design model parameters. Models of two important classes of nonsingular Gaussian (NG) CM sequences, called $CM_L$ and $CM_F$ models, and a model of the NG reciprocal sequence, called reciprocal $CM_L$ model, were presented in our previous works and their applications were discussed. In this paper, these models are studied in more detail, in particular their parameter design. It is shown that every reciprocal $CM_L$ model can be induced by a Markov model. Then, parameters of each reciprocal $CM_L$ model can be obtained from those of the Markov model. Also, it is shown that a NG $CM_L$ ($CM_F$) sequence can be represented by a sum of a NG Markov sequence and an uncorrelated NG vector. This (necessary and sufficient) representation provides a basis for designing parameters of a $CM_L$ ($CM_F$) model. From the CM viewpoint, a representation is also obtained for NG reciprocal sequences. This representation is simple and reveals an important property of reciprocal sequences. As a result, the significance of studying reciprocal sequences from the CM viewpoint is demonstrated. A full spectrum of dynamic models from a $CM_L$ model to a reciprocal $CM_L$ model is also presented. Some examples are presented for illustration.